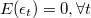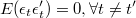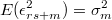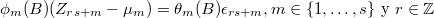Milestone Periodic ARMA Models
No date set
Decimos que un proceso 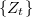 de segundo orden es periódicamente correlacionado con período
de segundo orden es periódicamente correlacionado con período  si sus dos primeros momentos son funciones periódicas de período
si sus dos primeros momentos son funciones periódicas de período  :
:
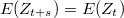
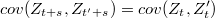
si el período 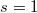 entonces tenemos un proceso estacionario de segundo orden.
entonces tenemos un proceso estacionario de segundo orden.
Una clase importante de modelos para describir tales periodicidades en la media y las covarianzas es la clase de modelos autoregresivos y medias móviles periódicos (PARMA). Los modelos PARMA son una extension de los modelos ARMA en el sentido de que admiten una representación de los parámetros del modelo variable en el tiempo.
Esta clase de modelos aparece con frecuencia en áreas donde las observaciones manifiestan comportamientos periódicos en las medias, varianzas y covarianzas, por ejemplo: hidrología, economía, consumo eléctrico, climatología y consumo de medios de prensa (Bayes).
Un proceso periódico estacionario 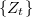 con periodo
con periodo  sigue un modelo PARMA con período
sigue un modelo PARMA con período  y parámetros en la estación (season)
y parámetros en la estación (season) 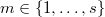 :
:
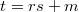
- media
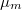
- polinomio AR
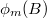 de grado
de grado 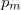
- polinomio MA
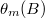 de grado
de grado 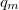
- varianza
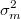
denotado por 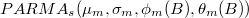 si existe un proceso
si existe un proceso
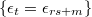 tal que:
tal que:
y el proceso 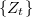 satisface la ecuacion en diferencias:
satisface la ecuacion en diferencias:
Este milestone es el punto de arranque para definir tickets asociados a los modelos PARMA. Estos tickets caen en diferentes categorías:
- Especificación de proceso PARMA en TOL.
- Evaluación de modelos PARMA y generación de procesos PARMA
- Evaluación de la verosimilitud de un proceso PARMA
- Estimación máximo-verosimil de parámetros para un proceso PARMA.
- Simulación de la distribución condicional completa de los parámetros de un proceso PARMA.
- Mecanismos de diagnosis para un proceso PARMA.