close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Opened 14 years ago

Last modified 14 years ago

#1049 accepted task

[BysSampler] Post-procesado de cadenas de Markov — at Version 1

Reported by: Víctor de Buen Remiro Owned by: Víctor de Buen Remiro
Priority: normal Milestone: TOL Packages
Component: Math Version:
Severity: normal Keywords:
Cc:

Description (last modified by Víctor de Buen Remiro)

Los métodos tradicionales de post-procesado basados en el burn-in y el thinning son demasiado arbitrarios para poder parametrizarlos de forma automática sin intervención del usuario.

Las cadenas simuladas con BysSampler cuentan con una ventaja adicional al conocerse la log-likelihood de cada muestra, pues esto permite contrastarla directamente con la densidad local empírica de los puntos cercanos que han sido generados en sus cercanías.

En una cadena perfectamente muestreada el número de puntos generados en torno a un punto dado debería ser proporcional a la verosimilitud media alrededor de dicho punto. Esto permite diseñar un criterio completamente objetivo para eliminar puntos de zonas sobre-muestreadas y sustituirlos por puntos en otras zonas infra-muestreadas.

Una posibilidad sería utilizar el algoritmo KNN para encontrar los k vecinos más próximos cada punto 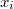x_{i}

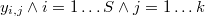
y_{i,j} \wedge i=1 \dots S \wedge j=1 \dots k

Si

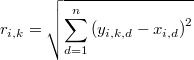
r_{i,k}=\sqrt{\underset{d=1}{\overset{n}{\sum}}\left(y_{i,k,d}-x_{i,d}\right)^{2}}

es la distancia de cada punto de la muestra a su k-ésimo vecino más próximo, la densidad local empírica en dicho punto será

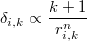
\delta_{i,k} \propto \frac{k+1}{r_{i,k}^{n}}

mientras que la verosimilitud media en ese entorno será

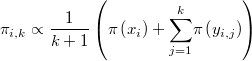
\pi_{i,k} \propto \frac{1}{k+1}\left(\pi\left(x_{i}\right)+\underset{j=1}{\overset{k}{\sum}}\pi\left(y_{i,j}\right)\right)

La diferencia de los logaritmos de ambas magnitudes sería
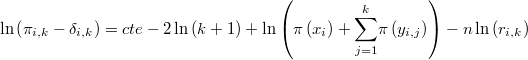
\ln\left(\pi_{i,k}-\delta_{i,k}\right)=cte-2\ln\left(k+1\right)+\ln\left(\pi\left(x_{i}\right)+\underset{j=1}{\overset{k}{\sum}}\pi\left(y_{i,j}\right)\right)-n\ln\left(r_{i,k}\right)

y su esperanza es 0. Si establecemos la bastante razonable hipótesis de normalidad tendríamos que

\ln\left(\pi\left(x_{i}\right)+\underset{j=1}{\overset{k}{\sum}}\pi\left(y_{i,j}\right)\right)\sim N\left(\mu,\sigma{2}\right)

con media y varianza desconocidas.

Si suponemos que la cadena de partida no está perfectamente equilibrada pero sí ha recorrido el espacio convenientemente, entonces podemos buscar los outliers de las magnitudes anteriores, eliminando los puntos con residuos muy negativos pues corresponden a zonas superpobladas.

Por el contrario, en los residuos muy positivos hay carencia de muestras por lo que es recomendable incluir nuevos puntos en esa zona. Para ello se puede utilizar un método multiple-try iniciado en el punto central del entorno y generar una serie corta.

Change History (1)

comment:1 Changed 14 years ago by Víctor de Buen Remiro

Description: modified (diff)
Note: See TracTickets for help on using tickets.