close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Opened 17 years ago

Closed 17 years ago

Last modified 17 years ago

#662 closed defect (fixed)

ARMAProcess::Eval.Almagro fails sometimes — at Version 5

Reported by: Víctor de Buen Remiro Owned by: Víctor de Buen Remiro
Priority: highest Milestone: Numerical methods
Component: Math Version: 1.1.7
Severity: blocker Keywords: ARMA, likelihood evaluation, BSR
Cc:

Description (last modified by Víctor de Buen Remiro)

In ​tol_tests/tol/random_generation/test_0005/test.tol there is a test for random generation of parameters of a linear regression with ARMA noise.

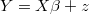
Y = X \beta + z $$
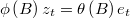
\phi\left(B\right) z_t = \theta\left(B\right) e_t $$
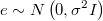
e \sim N\left(0,\sigma^{2} I\right) $$

It generates a set of independent vectors 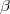\beta $$ and it calculates their logarithm of density.

First, the generalized linear regression is normalized by means of Cholesky decomposition of ARMA covariance

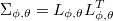
\Sigma_{\phi,\theta} = L_{\phi,\theta} L_{\phi,\theta}^{T} $$

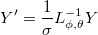
Y' = \frac{1}{\sigma} L_{\phi,\theta}^{-1} Y $$
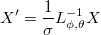
X' = \frac{1}{\sigma} L_{\phi,\theta}^{-1} X $$
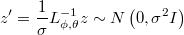
z' = \frac{1}{\sigma} L_{\phi,\theta}^{-1} z \sim N\left(0,\sigma^{2} I\right) $$

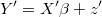
Y' = X' \beta + z' $$

Calculating Cholesky decomposition

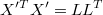
X'^{T} X' = L L^{T} $$

we have that

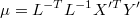
\mu = L^{-T}L^{-1}X'^{T} Y' $$
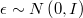
\epsilon \sim N\left(0,I\right) $$
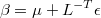
\beta = \mu + L^{-T} \epsilon $$

Obviously, logarithm of density of 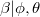\beta | \phi,\theta $$ is the same than for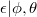 \epsilon | \phi,\theta $$

logDens\left(\beta| \phi,\theta\right) = logDens\left(\epsilon | \phi,\theta\right) = \sum_{k=1}^n{ \frac{1}{\sqrt{2\pi}}exp\left(\frac{\epsilon_k^2}{2}\right)} $$

Now, if we calculate ARMA noise corresponding for simulated 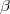\beta $$

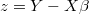
z = Y - X \beta $$

From Bayes theorem, logarithm of density of 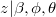z | \beta,\phi,\theta $$ matches

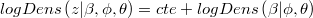
logDens\left(z | \beta,\phi,\theta\right) = cte + logDens\left(\beta| \phi,\theta\right) $$

TOL has two methods to calculate likelihood of an ARMA noise, ARIMALevinsonEval and ARIMAAlmagroEval (or alternatively ARMAProcess::Eval.Almagro). Well, ARIMALevinsonEval matches perfectly the given relation but ARIMAAlmagroEval fails sometimes.

Change History (5)

comment:1 Changed 17 years ago by Víctor de Buen Remiro

Description: modified (diff)
Status: new → assigned

comment:2 Changed 17 years ago by Víctor de Buen Remiro

Resolution: → fixed
Status: assigned → closed

(In [777]) Fixing bug in calculation of _.cov_za at function Eval.Almagro
Fixes #662

comment:3 Changed 17 years ago by Víctor de Buen Remiro

(In [778]) Fixing bug in calculation of cov_za at function CalcLikelihood_Almagro
Fixes #662

comment:4 Changed 17 years ago by Víctor de Buen Remiro

Description: modified (diff)

comment:5 Changed 17 years ago by Víctor de Buen Remiro

Description: modified (diff)
Note: See TracTickets for help on using tickets.