close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Version 11 (modified by lcereceda, 14 years ago) (diff)

--

TOL Package BysVecLinReg

BysVecLinReg yields for Bayesian simulator of Vectorial Linear Regression with arbitrary constraining inequations.

The method used to solve it in this package is based on ​https://www.tol-project.org/export/HEAD/tolp/OfficialTolArchiveNetwork/BysVecLinReg/doc/bayes-linear-minka.pdf Bayesian linear regression Thomas Minka (2001)] using invariant scale prior over 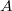A and inverse prior over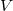 V

Vectorial linear regression

Vectorial linear regression equations are

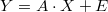
Y=A \cdot X + E

where

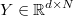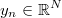
  • Y\in\mathbb{R}^{d\times N} is the multivariant known output matrix, where each row is a different output vector y_{n}\in\mathbb{R}^{N}
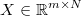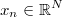
  • X\in\mathbb{R}^{m\times N} is the known and full rank input matrix, where each row is a different input vector x_{n}\in\mathbb{R}^{N}
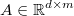  • A\in\mathbb{R}^{d\times m} has the unknown regression coefficients that we want to estimate
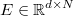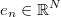  • E\in\mathbb{R}^{d\times N} is the multivariant residuals, where each row is the residuals vector e_{n}\in\mathbb{R}^{N} corresponding to output y_{n}

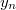
All residuals inside the same row are incorrelated normal, but residuals in the same column 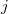j are

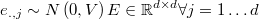
e_{.,j} \sim N\left(0,V\right) E\in\mathbb{R}^{d\times d} \forall j=1 \ldots d

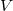where V is symmetric positive definite and unknown, but the same for each column.

Minka defines also the known data pair 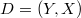D = \left(Y,X \right) that will be used just to get more compact conditioninig expressions.

Arbitrary constraining inequations

We will extend the model scope with arbitrary non null meassured restrictions over parameters inside 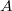A by means of adding a set of r inequations defining a feasible region

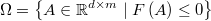
\Omega = \left\{ A\in\mathbb{R}^{d\times m} \mid F\left(A\right) \le 0 \right\}

with

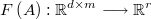
F\left(A\right):\mathbb{R}^{d\times m}\longrightarrow\mathbb{R}^{r}

being the arbitrary constraining function.

Invariant-scale prior over coefficient matrix

Although Minka does not explicitly state this, from the invariant prior it follows that 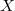X must be full-rank 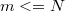m <= N because 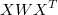X W X ^ T must be nonsingular with 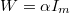W = \alpha I_{m}, where 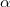\alpha is the scale-invariant parameter governing the prior and estimated more forward to maximize the evidence of the data, which depends on the assumptions of the model.

Inverse Wishart prior over covariance matrix

...