| Version 14 (modified by , 15 years ago) (diff) |
|---|
Generación de candidatos factibles en un politopo
Descripción del problema
Si tenemos que generar muestras que cumplan una serie de restricciones de desigualdad lineal
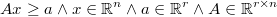
caben dos posibilidades:
- utilizar un generador de candidatos que cumpla las restricciones por construcción
- usar uno libre y luego rechazar los candidatos no factibles.
La ventaja de la segunda es que puede ser simétrico y evita el cálculo de la verosimilitud del candidato, pero el problema es que puede ser que tarde mucho en encontrar uno factible si el punto actual está demasiado cerca de la frontera, lo cual será muy habitual si el punto de máxima verosimilitud se encuentra fuera del politopo definido por las anteriores inecuaciones.
En la siguiente figura se observa un caso en el que el punto máximo verosímil sin restricciones (en verde) se encuentra fuera del politopo (en gris), por lo que el punto máximo-verosimil restringido (en rojo) se encuentra en la frontera del politopo. Las elipses verdes son líneas isoprobables, es decir con la misma densidad por lo que ese punto se encuentra en la intesección con el politopo de la mayor elipse externa al mismo. La cadena tenderá a estar cerca de ese punto y por tanto cerca de la frontera. Es evidente que cualquier entorno de generación simétrica de candidatos (en rosa), tendrá como máximo la mitad de área en la zona factible, lo cual es perfectamente asumible.
Es claro que no es preciso que el punto se encuentre en la frontera para que sus entornos tengan incluso menos de la mitad de sus puntos dentro del politopo, como ocurre con el entorno amarillo de la figura anterior. La pregunta es ¿qué pasaría si no estuviera en la frontera por inclumplir sólo una de las restricciones sino que incumpliera varias al mismo tiempo? Pues que la probabilidad de generar un punto factible decrecería exponencialmente, dependiendo también de los ángulos formados por los hiperplanos que definen cada restricción. Y eso ya no es asumible a nada que se tengan 3 ó mas restricciones incumplidas. En dos dimensiones sólo se pueden cruzar dos restricciones activas al mismo tiempo pero es fácil de extrapolar lo que ocurriría en espacios de dimensiones más altas:
Diseños de generadores de candidatos factibles
Se hace necesario por lo tanto disponer de generadores de candidatos que por construcción estén siempre dentro del politopo, es decir generadores de candidatos factibles. Tal generador no podrá ser simétrico por lo que será necesario no sólo poder generar muestras sino también calcular su densidad de una forma eficiente.
Definiciones
Dado un punto  estrictamente interior al politopo
estrictamente interior al politopo
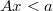
la distancia al 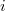 -ésimo hiperplano viene dada por la fórmula
-ésimo hiperplano viene dada por la fórmula
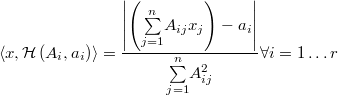
Llamaremos distancia de un punto a la frontera del politopo a la menor de las distancias a cada uno de sus hiperplanos, la cual por ser el punto interior ha de ser forzosamente positiva
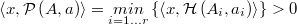
Paseo aleatorio hiperesférico
Se propone en primer lugar utilizar un generador con distribución uniforme en una hiperesfera centrada en el último punto generado y que esté incluida estrictamente en el politopo lo cual será cierto si el radio es menor que la distancia del punto a la frontera:
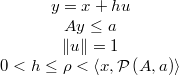
Al igual que se hace con los generadores simétricos habituales es necesario fijar un tamaño de paso
máximo  para que se generen puntos no demasiado lejanos del acutual, de forma
que el ratio de aceptación sea razonable.
De esta forma se podría definir el radio de la hiperesfera como
para que se generen puntos no demasiado lejanos del acutual, de forma
que el ratio de aceptación sea razonable.
De esta forma se podría definir el radio de la hiperesfera como
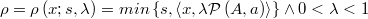
Para poder muestrear puntos cercanos a la frontera sería conveniente que 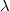 fuera cercano a 1, pero no tanto como para que los candidatos se quedaran demasiado cerca de ésta,
obligando a que el radio se estrechara cada vez más.
fuera cercano a 1, pero no tanto como para que los candidatos se quedaran demasiado cerca de ésta,
obligando a que el radio se estrechara cada vez más.
Función de densidad
La densidad del generador será porporcional al inverso del volumen de la hiperesfera y su logaritmo será, salvo una constante
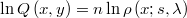
el cual depende de la posición del punto de partida respecto a las fronteras del politopo y no es por tanto un generador simétrico necesariamente, auqnue sí puede serlo eventualmente si el la distancia del punto a la frontera es menor que el tamaño de paso actual.
Función generatriz
Para generar un candidato 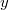 a partir del actual
a partir del actual  con esta
distribución se procederá como sigue
con esta
distribución se procederá como sigue
- Si el último punto generado es estrictamente interior al politopo y su distancia a la frontera es
mayor que cierta cota prefijada
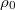 entonces usamos dicho punto como origen
de candidatos
entonces usamos dicho punto como origen
de candidatos
- Primero se simulará un vector multinormal estandarizado
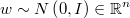
- Dividiendo ese vector por su norma euclídea se obtendrá una dirección unitaria uniforme en la frontera
de la hiperesfera de radio 1 centrada en el origen
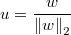
- Luego se multiplica ese vector por un radio
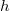 con densidad directamente
proporcional a la hipersuperficie de dimensión n-1 de la hiperesfera correspondiente
con densidad directamente
proporcional a la hipersuperficie de dimensión n-1 de la hiperesfera correspondiente
![\begin{array}{c} F\left(h\right)=\intop_{0}^{h}c\cdot t^{n-1}\mathbf{d}t=\left.\frac{c}{n}t^{n}\right]_{0}^{h}=\frac{c}{n}h^{n}\\ F\left(\rho\right)=\frac{c}{n}\rho^{n}=1\Rightarrow c=n\rho^{-n}\\ F\left(h\right)=\left(\frac{h}{\rho}\right)^{n}\end{array}](../chrome/site/images/latex/d63ea1bc478adbfb4b9af95021493d7d.png)
- Primero se simulará un vector multinormal estandarizado
- Si el punto está en la frontera o a una distancia menor de
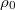 entonces se
retomará el último punto interior que cumplía dicha condición como origen de los
candidatos, y se ejecuta desde el principio el proceso, pero luego se compararán las probabilidades
de los candidatos con las del último punto generado, para asegurar así la convergencia, según el
principio básico del balance-detallado.
entonces se
retomará el último punto interior que cumplía dicha condición como origen de los
candidatos, y se ejecuta desde el principio el proceso, pero luego se compararán las probabilidades
de los candidatos con las del último punto generado, para asegurar así la convergencia, según el
principio básico del balance-detallado.
Paseo aleatorio radial asimétrico
Otra forma similar a la anterior pero que podría adaptarse mejor caundo el punto se acerca demasiado a la frontera, e incluso es válido si está en la propia frontera.
Se trataría de tomar una dirección unitaria aleatoria 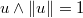 ,
siguiendo los mismos dos pasos del punto anterior, y luego encontrar un intervalo en esa dirección que incluya
al punto actual pero no necesariamente centrado en él, para generar el candidato uniforme en dicho intervalo
,
siguiendo los mismos dos pasos del punto anterior, y luego encontrar un intervalo en esa dirección que incluya
al punto actual pero no necesariamente centrado en él, para generar el candidato uniforme en dicho intervalo
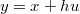
![h \sim U\left[h^{-},h^{+}\right] \wedge h^{-} \le 0 \le h^{+}](../chrome/site/images/latex/d06fd2abcda4f61de054ed1ebd2dce4d.png)
Los pasos para conseguirlo serían los siguientes
- Si estamos en un punto interior:
- Si los puntos
 y
y 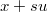 son ambos factibles
entonces se toma
son ambos factibles
entonces se toma 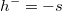 y
y 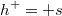
- Si
 no es factible habría que buscar mediante un método univariante
como el de la bisectriz o el de Fibonacci el mínimo valor de
no es factible habría que buscar mediante un método univariante
como el de la bisectriz o el de Fibonacci el mínimo valor de 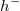 para el
que el punto es factible, y que debe estar obligatoriamente en el intervalo
para el
que el punto es factible, y que debe estar obligatoriamente en el intervalo
![\left[-s,0\right]](../chrome/site/images/latex/d6723dfade6196f1939142d66af9e18e.png)
- Análogamente, si
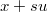 no es factible habría que buscar el máximo valor
de
no es factible habría que buscar el máximo valor
de 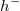 para el que el punto es factible, y que debe estar obligatoriamente
en el intervalo
para el que el punto es factible, y que debe estar obligatoriamente
en el intervalo ![\left[0,s\right]](../chrome/site/images/latex/13fe613f6d7fb6d76e8da196fac2e6f4.png)
- El intervalo ha de ser propio por partir de un punto interior, es decir,
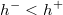 , con lo que ya se puede generar la uniforme anterior.
, con lo que ya se puede generar la uniforme anterior.
- Si los puntos
- Si el punto está en la frontera se tomará el último punto interior aceptado como origen de los candidatos y se repite desde el principio generando una nueva dirección unitaria aleatoria, pero se compararán las probabilidades de los candidatos con las del último punto generado, para asegurar así la convergencia.
Paseo aleatorio mixto
El paseo aleatorio hiperesférico tiene la ventaja de ser muy rápido pues sólo se necesita la distancia a la frontera, pero tiene el inconveniente que no es capaz de acercarse demasiado a la frontera y menos aún a los vértices donde a veces podría concentrarse la verosimilitud.
El paseo aleatorio radial asimétrico tiene la ventaja de que puede acercarse mucho más a la frontera pero resulta mucho más caro de evaluar, pues puede precisar resolver hasta dos problemas de optimización univariante para cada generación y para cada evaluación de la log-densidad.
Si dos métodos de generar cadenas de Markov cumplen la propiedad del balance-detallado entonces cualquier mezcla de ellas también la cumple, por lo que es perfectamente lícito alternar ambos métodos según convenga.
En este caso podría utilizarse el método hiperesférico cuando el punto se ecuentre a una distancia mínima de la frontera y el método radial asimétrico en otro caso.



