Package NonLinGloOpt

Este paquete TOL una API para usuario final al sistema de optimización global no lineal ​NLopt de Steven G. Johnson.

Definición del problema

El tipo de problemas que resuelve este sistema se puede formular matemáticamente del siguiente modo generalizado:

Se quiere maximizar una función objetivo arbitraria:

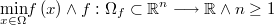
Sujeta a las siguientes

• Restricciones de intervalo:
  
  
  
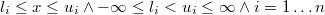
  Si una variable no tuviera cota inferior entonces sería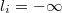 y si no tuviera cota superior entonces sería 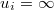A la región
  
  
  
  se le llamará hiperrectángulo de búsqueda y en el caso de optimización global deberá ser siempre acotado en todas las dimensiones.
  
  
• Restricciones de desigualdad arbitrarias:
  
  
  
  
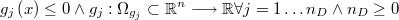
• Restricciones de igualdad arbitrarias:
  
  
  
  

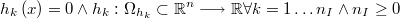
A la región del espacio 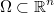de los puntos que cumplen todas las restricciones del problema le llamaremos región de factibilidad del problema. A los puntos de dicha región les llamaremos factibles o interiores y al resto no factibles o exteriores.

Hay una condición que se suele sobreentender por su obviedad, pero que es a veces la causa de que no funcionen los algoritmos: un punto factible debe pertenecer al dominio de la función objetivo, y al de las funciones de restricción, o sea:

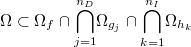
Por ejemplo, si en la función objetivo aparece el logaritmo de una variable se debe incluir alguna restricción o conjunto de ellas que obligue a que dicha variable sea positiva. Evidentemente, si no hay restricciones, pues todas ellas son en principio opcionales, el dominio de la función objetivo debe ser todo el espacio 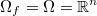. Obsérvese que si lo que se quiere es minimizar la función objetivo basta con tomar la función opuesta .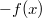

Nótese que a ninguna de las funciones se le ha exigido ser diferenciable, y ni tan siquiera ser continua; aunque, como se verá más tarde, el usuario deberá informar de qué clase analitica es el problema para poder saber qué métodos son aplicables.

En lo que afecta a este sistema, la clase analítica de una función ha de ser la máxima de las condiciones cumplidas por la función de entre las siguientes

Arbitraria	Real ARBITRARY = -1	si la función no es continua.
Continua	Real CONTINUOUS = 0	si la función es continua pero no diferenciable.
Diferenciable	Real DIFFERENTIABLE = 1	si la función es continua y diferenciable sólo una vez.
Doblemente diferenciable	Real TWICE_DIFFERENTIABLE = 2	si la función es continua y al menos doblemente diferenciable.

La clase analítica del problema será la mínima de entre las de su funciones objetivo y las de sus restricciones de igualdad y desigualdad. El usuario debe conocer esta característica del problema para informarlo en su definición.

Guia del usuario

Los problemas se definirán como una instancia de Class @Problem definida en problem.tol

Formulación de funciones objetivo y de restricción

Tanto si se calcula el gradiente como si no, las funciones objetivo y las de restricción deben tener la API TOL general común a todas ellas:

Real eval (Matrix x, Matrix gradient)

siendo tanto x como gradient matrices de n filas y 1 columna.

Aún en el caso de que se quiera usar un método que precise el gradiente, no necesariamente se exigirá calcular el mismo cada vez que se quiera evaluar la función. En tales casos se le pasará la matriz vacía para indicar que no se haga el cálculo. Podría pensarse si no sería mejor hacer una función para la evaluación de la función y otra para el gradiente, pero resulta que muy a menudo el cálculo del gradiente utiliza en parte las mismas componentes que la propia función, por lo que resulta más eficiente que se calculen de forma conjunta. La función de evaluación debería por tanto tener este aspecto:

Real eval (Matrix x, Matrix gradient)
{
  ...
  Real y = ...;
  Real If(Rows(gradient), {
    ...
    Matrix gradient := ...;
    True
  });
  y
};

Si el problema no es diferenciable o el cálculo del gradiente es muy costoso y se van a usar sólo algoritmos que no requieren el cálculo del gradiente, entonces se puede hacer caso omiso del argumento Matrix gradient y calcular sólo el valor de la función.

A veces es conveniente que las funciones del problema se definan como métodos de una clase, bien porque manejan información auxiliar compleja, bien porque se trate de funciones pertenecientes a una familia paramétrica y sea más cómodo implementarlas de este modo. En esos casos, el método es un objeto TOL común a todas las instancias de la clase, por lo que no es suficiente por sí misma y habrá que pasar también la instancia de la clase para la que queremos evaluar, y lo haremos mediante un conjunto como éste

[[NameBlock owner, Code owner::method ]]

Características obligatorias en la definición del problema

Las siguientes características del problema deben ser cumplimentadas por el usuario de forma obligatoria y deben ser congruentes entre sí.

//If you sign ==- 1 minimized, and if sign == 1 maximizes
  Real sign;         
  
//If true, a global optimal point will be searched. Else just a 
//local one.
  Real neededGlobal;  
 
//Minimum analytical class of target and constraining functions must be one
//of elements of 
//Set NonLinGloOpt::AnalyticalClass =
//{[[
//  Real ARBITRARY            = -1,  // Arbitrary functions
//  Real CONTINUOUS           =  0,  // Class C_0: Continuous
//  Real DIFFERENTIABLE       =  1,  // Class C_1: Differentiable
//  Real TWICE_DIFFERENTIABLE =  2   // Class C_2: Twice differentiable
//]]};
  Real id_analyticalClass;

//Indicates if the gradient known or unknown in an analytical or 
//numerical way. Must be one element of 
//Set NonLinGloOpt::GradientKnowneledge =
//[[
//Real NONE        = 0,  //Doesn't exists or it's too hard to calculate
//Real ANALITICAL  = 1,  //Use analitical gradient
//Real NUMERICAL   = 2   //Use numerical gradient
//]];
  Real id_useGradient;  
  
//Target function could be a simple Code or a class method of an
//instance owner.
// - Real target(Matrix x, Matrix gradient)
// - Set target = [[NameBlock owner, Code method]]
//When argument gradient is not empty, then the function, or the 
//method must update it. 
  Anything target;

//Initial values of variables 
  Matrix x0;        

Características opcionales en la definición del problema

Hay otra serie de carcterísticas del problema que son opcionales pues o bien tienen un valor por defecto predefinido o bien existe un método interno que les da un valor adecuado.

//Optimization method. If not specified the system will choose one
//by calling method select_automatic_algorithm
  Real id_algorithm = ?;  //Numerical identifier NonLinGloOpt::Algorithm
  Text co_algorithm = ""; //Codified name

//Lower bounds of the variables (-1/0 if none)
  Matrix lower_bounds = Rand(0,0,0,0); 

//Variable upper bounds (+1/0 if none)
  Matrix upper_bounds = Rand(0,0,0,0);

//Set of inequality constraints g(x)<=0
//Conjunto de elementos Code o [[NameBlock owner, Code target]] para métodos
//Constraining function could be a simple Code or a class method of an
//instance owner.
// - Real g (Matrix x, Matrix gradient)
// - Set g = [[NameBlock owner, Code method]]
//When argument gradient is not empty, then the function, or the 
//method must update it. 
  Set inequations = Copy(Empty); 

//Set of equality constraints h(x)<=0
//Conjunto de elementos Code o [[NameBlock owner, Code target]] para métodos
//Constraining function could be a simple Code or a class method of an
//instance owner.
// - Real h (Matrix x, Matrix gradient)
// - Set h = [[NameBlock owner, Code method]]
//When argument gradient is not empty, then the function, or the 
//method must update it. 
  Set equations = Copy(Empty);   

//Tolerance for the evaluation of inequality constraints
  Real inequationTolerance = 1E-8;

//Tolerance for the evaluation of the equality constraints
  Real equationTolerance = 1E-8;

//Relative tolerance of the stop criteria
  Real relativeTolerance = 1E-6; 

//Maximum run time
  Real maxTime = ?;

//If verboseEach>0, evaluation of target funciton will be traced 
//each the specified number of evaluations.
  Real verboseEach = 100;

Creación y lanzamiento de la optimización

Una vez definido un problema hay que crear el motor de optimización como una instancia de Class @Opt definida en opt.tol

//Creating the optimizer instance
NonLinGloOpt::@Opt opt = problem::create_optimizer(?);

y finalmente se llamará al método de optimización para que ejecute el algoritmo

//Running the optimization
Real opt::optimize_problem(problem);

Entre medio de ambas acciones, el usuario avanzado puede retocar la instancia opt mediante los métodos de @Opt, cada uno de los cuales implementa los métodos de la clase C++ interna nlopt::opt cuya API puede verse ​aquí Estos métodos pueden leerse directamente en el código TOL o exporarse en la interfaz de TOLBase.

Tutorial

La mejor forma de aprender a usar cualquier cosa es empezar a usarla de forma controlada, para lo cual se dispone de una batería de ejemplos a disposición de los usuarios.

Función objetivo bivariante no lineal con restricciones de desigualdad no lineal

En primer lugar se expondrá el ​ejemplo proporcionado en el tutorial de NLopt

Se quiere encontrar un mínimo local de la función objetivo:

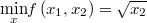
Sujeta a las

• restricciones de intervalo:
  
  
  
  
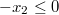
• y a las restricciones de desigualdad:
  
  
  
  
  

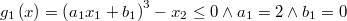
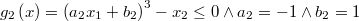
Nótese cómo se han reescrito las inecuaciones de restricción en la forma canónica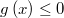

El punto inicial de la búsqueda es el punto factible

Obsérvese que se trata de un problema al menos dos veces diferenciable.

El código TOL completo de este ejemplo está disponible aquí

A continuación veremos ese mismo código por partes

Función objetivo

Obérvese cómo la función objetivo incluye la evaluación condicional del gradiente y cómo ésta hace uso de los cálculos empleados en evaluar la propia función.

////////////////////////////////////////////////////////////////////////////////
//Target function defined as simple code
Real my_function(Matrix x, Matrix grad)
////////////////////////////////////////////////////////////////////////////////
{
  Real y = Sqrt(MatDat(x,2,1));
  Real If(Rows(grad), {
    Matrix grad := Col(0.0,0.5/y);
    True
  });
  y
};

Restricciones de desigualdad

Como ambas restricciones de desigualdad responden a un mismo patrón es conveniente no repetir su formulación usando una clase para su definición.

////////////////////////////////////////////////////////////////////////////////
//When a set of constraining functions are part of a parametric family
//of funcitons we can define a class to make an easier definition
Class @my_inequation 
////////////////////////////////////////////////////////////////////////////////
{
  Real a;
  Real b;
  Real constraint(Matrix x, Matrix grad)
  {
    Real x1 = MatDat(x,1,1);
    Real x2 = MatDat(x,2,1);
    Real ax1b = a*x1 + b;
    Real If(Rows(grad), {
      Matrix grad := Col(3 * a * ax1b^2,-1.0);
      True
    });
    Real g = (ax1b^3 - x2);
    g
  }
};

////////////////////////////////////////////////////////////////////////////////
//Inequality constraining functions defined as class instances
////////////////////////////////////////////////////////////////////////////////
@my_inequation ineq1 = [[Real a= 2,Real b=0]];
@my_inequation ineq2 = [[Real a=-1,Real b=1]];

Definición del problema y sus características

//Don't forget require the package if it has still no been loaded
#Require NonLinGloOpt;

//Defining the problem
NonLinGloOpt::@Problem problem = [[
//Optimization method. If not specified the system will choose one
//by calling method select_automatic_algorithm
//In this case we want to use MMA (Method of Moving Asymptotes)
// http://ab-initio.mit.edu/wiki/index.php/NLopt_Algorithms#MMA_.28Method_of_Moving_Asymptotes.29 
  Real id_algorithm = NonLinGloOpt::Algorithm::LD_MMA;  
  //We want to minimize the target function
  Real sign = -1;
  //We want just a local minimum
  Real neededGlobal = False;
  //The problem is almost twice differentiable
  Real id_analyticalClass = 
    NonLinGloOpt::AnalyticalClass::TWICE_DIFFERENTIABLE;
  //The gradient of all functions is known 
  Real id_useGradient = True;
  //Target given as simple Code
  Anything target = my_function;
  //Lower bounds 
  Matrix lower_bounds = Col(-10,  0); //x1>=-10, x2 >= 0
  //Upper bounds 
  Matrix upper_bounds = Col( 10, 10); //x1<= 10, x2 <=10
  //There are two non linear constraining inequations 
  Set inequations = [[
   [[ineq1, ineq1::constraint]], //Inequation given by class method
   [[ineq2, ineq2::constraint]]  //Inequation given by class method
  ]];
  //Initial values
  Matrix x0 = Col(1.234, 5.678); 
  //Stopping criteria of relative tolerance for both x and y
  Real relativeTolerance = 1E-4; //
  //Stopping criteria of maximum running time
  Real maxTime = 60; 
  //Funcitons will be traced each this number of evaluations
  Real verboseEach = 1
]];

Creación y lanzamiento de la optimización

//Creating the optimizer instance
NonLinGloOpt::@Opt opt = problem::create_optimizer(?);

//Running the optimization
Real opt::optimize_problem(problem);

Guía del programador y del usuario avanzado

El sistema NLopt contiene 17 algoritmos principales con 41 variantes que intentan abarcar la mayor parte de los tipos de problemas tipo de la programación matemática no lineal y cuya descripción puede verse ​aquí de forma detallada.

Existen métodos para optimización local y global, para funciones no lineales arbitrarias, continuas o diferenciables y con restricciones de igualdad y desigualdad no lineal o sin ellas.

El valor añadido del paquete TOL NonLinGloOpt pretende ser un sistema experto que, en el caso de que el usuario no proponga un método específico, busque uno cuyas características sean compatibles con las del problema, a saber:

IsGlobal	0,1	Un método de optimización puede ser global o local, pero no ambas cosas a al vez, luego es determinante saber si se requiere un óptimo local o uno global para la selección del mismo.
AnalyticalClass	AR: Arbitrary, C0: Continuous, C1: Differentiable, C2: Twice differentiable	Es la clase analítica mínima capaz de tratar un algoritmo debe ser igual o mayor que la clase mínima de las funciones objetivo y de restricciones. Por ejemplo, si una de las funciones del problema es continua pero no diferenciable y todas las demás son diferenciables, la clase analítica del problema es C0 y sólo se podrán usar algoritmos e tipo AR ó C0, pero no los de tipo C1 ó C2. El usuario es el único que puede y debe ofrecer esta información acerca del problema.
NeedsGradient	0,1	Los algoritmos de tipo C1 ó C2 pueden o no necesitar realmente calcular el gradiente. Por otra parte el que un problema sea clase C1 ó C2 no implica que se conozca analíticamente el gradiente, aunque siempre se puede calcular numéricamente, pero en cualquier caso puede que el coste computacional sea excesivo. Así pues, tanto si el gradiente no existe (AR,C0), como si existe pero no tenemos un método rápido de obtenerlo, se debe elegir un algoritmo que no utilice el gradiente. Es responsabilidad del usuario comunicar al sistema esta característica del problema.
NeedsFeasiblePoint	0,1	Unos métodos precisan comenzar por un punto factible y otros no, y no siempre el usuario es capaz de proporcionar un punto adecuado. En estos casos el sistema debería utilizar un método que pueda comenzar por un punto exterior hasta encontrar uno interior y a partir de ahí se podría continuar con otro método cualquiera que fuera más eficiente. El propio sistema comprobará si la solución inicial proporcionada es factible.
NeedsBounds	0,1	En general todos los métodos globales precisan que se dé un intervalo de dominio a cada variable, es decir, que se defina un hiperrectángulo de búsqueda , mientras que los métodos locales no lo necesitan.
SupportsBounds	0,1	La mayoría de los métodos soportan intervalos de dominio pero no siemrpe es así, por lo que hay que tenerlo en cuenta.
SupportsInequalities	0,1	La mayoría de los métodos de optimización no soportan restricciones de desigualdad, aunque siempre existe la posibilidad de utilizar el método especial del Lagrangiano Aumentado para convertir el problema en otro sin restricciones que se pueda tratar con un método subsidiario adecuado.
SupportsEqualities	0,1	Sólo unos pocos métodos soportan restricciones de igualdad, aunque lo mism o que con las desigualdades se puede aplicar el método especial del Lagrangiano Aumentado. Concretamente se puede aplicar sólo a las restricciones de igualdad manteniendo las de desigualdad si hay un método adecuado que lo pueda resolver.
PreferredScale	S: Short [1...10], M: Medium [11...100], L: Large[101...1000] E: Extreme[1001...]	El número de variables con el que el algoritmo es capaz de tratar de forma eficiente

En la hoja de cálculo ​NLopt_algorithms se muestra un cuadro resumen de las características asociadas a cada variante algorítmica del paquete NLopt.

Se aconseja a los programadores y usuarios avanzados visitar de forma somera el código fuente del paquete que a veces es la mejor forma de familiarizarse con un sistema. Estos son los archivos principales del sistema:

• NonLinGloOpt.tol: Fichero raíz del paquete
• constant.tol: Constantes de codificación de algorimos, resultados, criterios de parada y otras características de la optimización y la definición de los problemas.
• problem.tol: Clase @Problem para la definición de problemas.
• opt.tol: Clase @Opt para la optimización de problemas mediante la API con NLOpt.
• CppTools.cpp: API C++ con NLOpt.