ROC curve

[Jorge]

The ROC curve is widely used in the diagnosis of qualitative response models.

In ​ROC (Wikipedia) we can find the definition.

We request the inclusion of this function and other derived values, such as Area Under Curve (AUC) in a TOL package. Consider also an implementation in C++ because its performance could impact when it is used with big models or when it should be invoked repeatedly from other computations such as "DUETO" decomposition.

Below is an implementation done in TOL (thanks to pgea and cgarcia):

//////////////////////////////////////////////////////////////////////////////
Real ROC.AUC(Matrix real, Matrix prediction) // by columns
//////////////////////////////////////////////////////////////////////////////
{
  Set steps = Sort(MatSet(Tra(prediction))[1], Compare);
  Real length = Rows(real);
  Real RP = MatSum(real);
  Real RN = length-RP;
  Real FFP = 1;
  Real AUC = 0;
  Set EvalSet(steps, Real (Real step) {
    Real FFP0 = FFP;
    Matrix mc = GE(prediction, step);
    Matrix mFP = mc $* Not(real);
    Real FP = MatSum(mFP);
    Real FFP := FP/RP;
    Real If(FFP<FFP0, {
      Matrix mVP = mc $* real;
      Real VP = MatSum(mVP);
      Real FVP = VP/RN;
      Real AUC := AUC - FVP*(FFP-FFP0);
    1});
  1});
  AUC
};

[Pedro Gea]

Cuando el tamaño de la matriz es grande, el cálculo exacto anterior es demasiado lento y podría aproximarse bien sobre una partición del intervalo [0, 1] utilizando algo como:

Set steps = Range(0, 1, 1/divisions);

[Víctor de Buen Remiro]

A mí me resulta completamente ininteligible el artículo ​ROC (Wikipedia). Lo único que he podido medio entender es que el AUC está relacionado estrechamente, aunque no dice cómo, con el test Mann–Whitney U, el cual sí está disponible en TOL mediante la función

Set AlgLib.MannWhitneyUtest(Matrix x, Matrix y)

También dice que es equivalente al test de rango de signos de Wilcoxon para dos muestras, aunque ese test sólo lo tenemos para una muestra

Set AlgLib.WilcoxonSignedRankTest(Matrix x, Real m)

Igual merece la pena buscar una implementación del de dos muestras pues sería algo más general que el AUC y resolvería el tema de la eficiencia.

Por ahora podemos meter la versión propuesta, pero primero, por favor, ¿podría alguien documentar medianamente esa función para saber al menos qué son y qué forma tienen los argumentos que espera? Tampoco estaría mal un ejemplo de uso para chequearla. Para meter las cosas en un paquete que va a usar la gente tenemos que cumplir unas normas mínimas de higiene. Si tenemos por ahí funcionando otras funciones relacionadas estaría bien ponerlas todas juntas.

Por las sentencias TOL que veo se adivina que se puede acelerar bastante en el propio TOL pero me gustaría entender que es lo que hace esa función realmente.

Por otro lado, sin menoscabo de incluir todos los estadísticos al uso que se quieran, yo lo que no perdería es el objetivo final de estas funciones, que no es otro que comparar modelos, y ahí yo creo que habría que adoptar un criterio bayesiano en lugar de basarse es estadísticos arbitrarios más o menos elegantes.

Entiendo que si el cliente está acostumbrado a ver esas cosas pues hay que darle gusto, pero lo que debe hacer un estadístico bayesiano en estos casos es buscar la función de coste, pues, por muy mala aproximación que se tenga de la misma, los resultados son necesariamente mucho menos subjetivos que con cualquier otro sistema de comparación.

[Alfredo Torre]

Por si sirve de ayuda, os dejo un NameBlock con una implementación en TOL de ROC: roc_v1.tol​

[Alfredo Torre]

Vuelvo a subir la función con un par de correcciones: roc_v2.tol​

[Alfredo Torre]

Disculpad. Subo de nuevo el NameBlock con otros pequeños cambios: roc_v3.tol​

[Víctor de Buen Remiro]

(In [4134]) Fixes #1350
Integrating NameBlock ROC in package QltvRespModel

[Víctor de Buen Remiro]

En la versión QltvRespModel.4.2 se incorpora el NameBlock QltvRespModel::ROC propuesto anteriormente.

El resultado de QltvRespModel::ROC::Curve tras una estimación se encuentra en
Set _.contrast::_.roc.Curve

En Set _.contrast::_.roc.Chart se reorganizan los resultados para ser dibujados desde TOLBase con la opción Todas contra la primera

En Real _.contrast::_.roc.AUC se devuelve el área bajo la curva.

[Pedro Gea]

Considérese el código en aucroc.tol​ e impleméntyense también los otros estadísticos como el índice KS o el índice de Gini.

Solicitud procedente del tique #702 de MMS.

[Pedro Gea]

(In [4978]) Refs #1350
Se incorporan dos funciones para el cálculo del AUC y el Gini sin pasar por la obtención de la curva.
Se implementa una clase para representar a una curva ROC interpolada: @InterpolationROC
que sustituye al nameblock ROC incorporado anteriormente.

[Pedro Gea]

Se adjunta un ejemplo de uso de la clase y funciones implementadas:

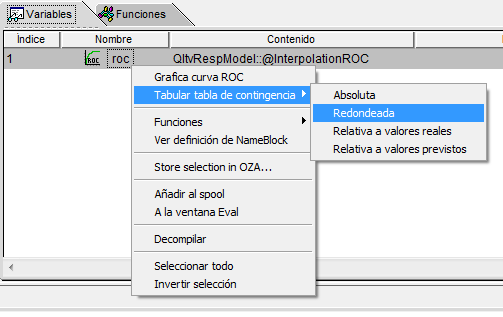
#Require QltvRespModel;

// Se obtienen unos datos de ejemplo:
Real PutRandomSeed(2143);
Matrix m = Rand(5000, 1, 0, 1);
Matrix mb = Round(m$*Rand(Rows(m), 1, 0, 1));

// Se obtienen el AUC y el Gini con las funciones directas:
Real auc = QltvRespModel::ROC.AUC(mb, m);
Real gini = QltvRespModel::ROC.Gini(mb, m);

// Se obtienen el AUC y el Gini con una curva interpolada con 500 puntos:
QltvRespModel::@InterpolationROC iROC = 
  QltvRespModel::@InterpolationROC::Default(mb, m, 500);
Real iAUC = iROC::GetAUC(?);
Real iGini = iROC::GetGini(?);

// Algunos estadísticos dependientes del umbral escogido. (ej: 0.75)
Real iROC::GetTPR(0.75); // True Positive Rate (TPR) (sensibilidad)
Real iROC::GetFDR(0.75); // False Discovery Rate (FDR)
Set iROC::GetContingencyTable(0.75);
Set iROC::GetContingencyTable.Rounded(0.75);
Set iROC::GetContingencyTable.ActualRelative(0.75);
Set iROC::GetContingencyTable.PredictedRelative(0.75);

[Pedro Gea]

Podría eliminarse el nameblock ROC que queda obsoleto si se considera conveniente.