close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Opened 16 years ago

Closed 13 years ago

#626 closed defect (fixed)

Plausible initial values for BSR chain

Reported by: Víctor de Buen Remiro Owned by: Víctor de Buen Remiro
Priority: normal Milestone: Numerical methods
Component: Math Version: 2.0.1
Severity: normal Keywords: BSR, Initial values, QuadProg
Cc:

Description

It's neccesary a generic method to get plausible initial values for BSR chain.

In this case Plausible means factible and no null density weighted.

At this moment problem is solved for small and medium scale models by means of QuadProg R package. In order to use it you should set these configuration parameters about initial values trying

    //Try order for constrained max likelihood solution to start MCMC
    Real bsr.iniVal.try.cnstrMLE = 1;
    //Try order for constrained minimum norm solution to start MCMC
    Real bsr.iniVal.try.cnstrMinNorm = 2;
    //Try order for given by user solution to start MCMC
    Real bsr.iniVal.try.givenByUser = 3;
    //Try order for zero solution to start MCMC
    Real bsr.iniVal.try.zero = 4;

Change History (10)

comment:1 Changed 16 years ago by Víctor de Buen Remiro

Keywords: BSR Initial values QuadProg added
Owner: changed from Jorge to Víctor de Buen Remiro
Status: new → assigned

Generic solution could be an specialization of QuadProg designed for large sparse matrices.

comment:2 Changed 16 years ago by Víctor de Buen Remiro

Priority: highest → high

comment:3 Changed 16 years ago by Víctor de Buen Remiro

Component: Database → Math

comment:4 Changed 16 years ago by Víctor de Buen Remiro

Severity: blocker → critical
Version: → 2.0.1

comment:5 Changed 16 years ago by Víctor de Buen Remiro

Milestone: → BSR Numerical methods

comment:6 Changed 15 years ago by Víctor de Buen Remiro

Resolution: → fixed
Status: assigned → closed

This feature has been added to the release v2.0.1 b.0.14.alpha

The problem is to find a point 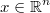x\in\mathbb{R}^{n} $$ matching a set of r $$ arbitrary coherent inequations defining a non empty polytope

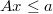
Ax\leq a $$
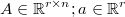
A\in\mathbb{R}^{r\times n}; a\in\mathbb{R}^{r} $$

We can write it as a non linear unrestricted optimization problem

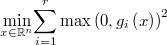
\underset{x\in\mathbb{R}^{n}}{\min}\overset{r}{\underset{i=1}{\sum}}\max\left(0,g_{i}\left(x\right)\right)^{2} $$

where

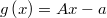
g\left(x\right)=Ax-a $$

The algorithm, a simplfied version of penalty exterior point of Ablow-Brigman method, has been implemented inside a new NameBlock Polytope as the member Polytope::Region::FindFeasible on file tolp/trunk/tol/stdlib/math/optim/LP/polytope.tol

User can force this option setting this configuration paramter

  //Try order for constrained arbitrary solution to start MCMC
  Real bsr.iniVal.try.findFeasible = 1;

comment:7 Changed 14 years ago by Víctor de Buen Remiro

Resolution: fixed
Status: closed → reopened

When dimension is high, dense methods included in QuadProg are not efficient or simply doesn't work.

Now we have package NonLinGloOpt that can be used with sparse matrices to find a minimum squares solution.

comment:8 Changed 14 years ago by Víctor de Buen Remiro

(In [3390]) Refs #626

comment:9 Changed 14 years ago by Víctor de Buen Remiro

Priority: high → normal
Severity: critical → normal

comment:10 Changed 13 years ago by Víctor de Buen Remiro

Resolution: → fixed
Status: reopened → closed
Note: See TracTickets for help on using tickets.