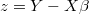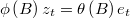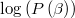In each iteration of BSR, we need to simulate vector 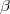 matching this linear constrained regression with ARIMA noise:
matching this linear constrained regression with ARIMA noise:
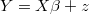
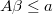
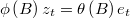
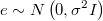
ARMA and variance parameters are changing in each iteration of BSR, and, if there are missing values or non linear filters matrices 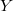 and
and 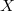 could also change in each iteration. Only constraining inequations remain invariant in any case.
could also change in each iteration. Only constraining inequations remain invariant in any case.
So, an ARIMA decomposition and filter and a Cholesky decomposition are needed in order to simulate linear block. Even if 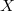 is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
I propose a preconditioning method to save a lot of time calculating and storing all blocks of a simulation only for one of a lot of iterations and using them to generate aproximations that will be refinated inside an internal Metropolis-Hastings chain.
The main idea behind this method is that, when external BSR Gibbs chain is already in convergence phase, difference of expected values between two different iterations should tend to zero. So, the simulator of a past iteration should be a good candidate generator for distribution of current iteration.
Let be the last full calculated and stored system
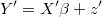
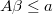
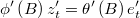
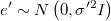
Following these steps for each Metropolis-Hastings step we can generate a candidate of vector 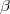 calculating simultaneously its exact density:
calculating simultaneously its exact density:
- Since this system has been previously decomposed is very fast to generate a candidate vector and its density
 , that is not depending on previous state.
, that is not depending on previous state.
- In order to calculate the density for current system we will get corresponding ARIMA noise
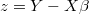
- By means of Levinson or Almagro method of ARMA evaluation it's posible to calculate in a very fast way differential equation
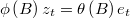
getting also residuals likelihood which logarithm is, but a constant, the exact density 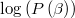
Due to candidates are independent of previous chain it is enought to have just one non rejected sample. When number of rejected iterations growns is the moment of remake full calculations and store a new preconditioner regression. If this happens after a large number of iterations, then a lot of time will be saved.
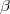 matching this linear constrained regression with ARIMA noise:
matching this linear constrained regression with ARIMA noise: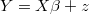
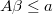
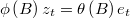
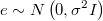
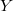 and
and 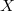 could also change in each iteration. Only constraining inequations remain invariant in any case.
could also change in each iteration. Only constraining inequations remain invariant in any case.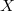 is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
is very sparse, after applying ARIMA filter it could become dense and process will be too slow.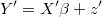
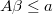
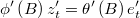
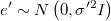
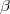 calculating simultaneously its exact density:
calculating simultaneously its exact density: , that is not depending on previous state.
, that is not depending on previous state.