Opened 17 years ago
Last modified 17 years ago
#664 closed enhancement
Preconditioned simulation of BSR linear block — at Version 11
| Reported by: | Víctor de Buen Remiro | Owned by: | Víctor de Buen Remiro |
|---|---|---|---|
| Priority: | highest | Milestone: | Numerical methods |
| Component: | Math | Version: | 2.0.1 |
| Severity: | major | Keywords: | BSR, linear, ARIMA, preconditioned |
| Cc: |
Description (last modified by )
In each iteration of BSR, we need to simulate vector 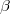 matching this linear constrained regression with ARIMA noise:
matching this linear constrained regression with ARIMA noise:
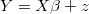
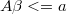
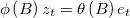
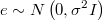
ARMA and variance parameters are changing in each iteration of BSR, and, if there are missing values or non linear filters matrices 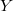 and
and 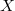 could also change in each iteration. Only constraining inequations remain invariant in any case.
could also change in each iteration. Only constraining inequations remain invariant in any case.
So, an ARIMA decomposition and filter and a Cholesky decomposition are needed in order to simulate linear block. Even if 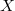 is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
is very sparse, after applying ARIMA filter it could become dense and process will be too slow.
I propose a preconditioning method to save a lot of time calculating and storing all blocks of a simulation only for one of a lot of iterations and using them to generate aproximations that will be refinated inside an internal Metropolis-Hastings chain.
The main idea behind this method is that, when external BSR Gibbs chain is already in convergence phase, difference of expected values between two different iterations should tend to zero. So, the simulator of a past iteration should be a good candidate generator for distribution of current iteration.
Let be the last full calculated and stored system
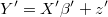
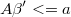
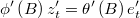
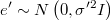
Following these steps for each Metropolis-Hastings step we can generate a candidate of vector 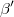 calculating simultaneously its exact density:
calculating simultaneously its exact density:
- Since this system has been previously decomposed is very fast to generate a pre-candidate vector
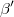 matching it
matching it
- The corresponding ARIMA noise is simply
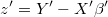
- By means of Almagro method it's posible to calculate residuals
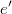 and initial values
and initial values 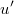 that solve difference equation
that solve difference equation
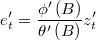
- Let be the standarized multinormal residuals
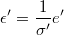
- Since
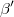 are determined by
are determined by 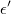 by means of a full range linear equation, their densities have constant ratio, and logarithm of density of candidate vector can be calculated directly as
by means of a full range linear equation, their densities have constant ratio, and logarithm of density of candidate vector can be calculated directly as
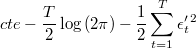
- Then we can propose residuals and initial values for current system as
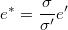
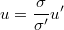
- ARIMA noise for current system becomes simply
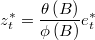
- In order to get the refined candidate, we will take minimum residuals solution of sparse linear system
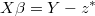
- In order to calculate its exact density, it will be obtained the ARIMA noise
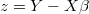 to get standarized residuals from ARIMA equations.
to get standarized residuals from ARIMA equations.
- If resulting vector doesn't match constraining inequations
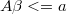
density will be toggled to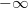 in order to force rejection.
in order to force rejection.
The number of internal Metropolis-Hastings non rejected iterations must be a parameter of user configuration and should not be more than 10 or 20 iterations. When number of rejected iterations growns is the moment of remake full calculations and store a new preconditioner regression. If this happens after a large number of iterations, then a lot of time will be saved.
Change History (11)
comment:1 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:2 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:3 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:4 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:5 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:6 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:7 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:8 Changed 17 years ago by
| Description: | modified (diff) |
|---|---|
| Status: | new → assigned |
comment:9 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:10 Changed 17 years ago by
| Description: | modified (diff) |
|---|
comment:11 Changed 17 years ago by
| Description: | modified (diff) |
|---|
