#718 closed defect (fixed)
Logit function returns wrong probability
| Reported by: | César Pérez Álvarez | Owned by: | Víctor de Buen Remiro |
|---|---|---|---|
| Priority: | highest | Milestone: | Mantainance |
| Component: | Math | Version: | |
| Severity: | critical | Keywords: | |
| Cc: |
Description
Hi,
when I was used Logit function and a log message is like this:
2009/07/23 17:31:24 :
Empieza Logit model (46212x44)
Logit model iteration(0) LogLikelyhood = -32031.71750800246 maxAbsDif = 1.806530388564703 Gradient Norm = 3041.715167005722 Tiempo : 3.188 segundos
Logit model iteration(1) LogLikelyhood = -24056.38553091559 maxAbsDif = 0.7096645080192925 Gradient Norm = 903.1248844663231 Tiempo : 3.172 segundos
Logit model iteration(2) LogLikelyhood = -1.#INF maxAbsDif = 0.6107093713189264 Gradient Norm = 252.949584659891 Tiempo : 3.187 segundos
Logit model iteration(3) LogLikelyhood = -1.#INF maxAbsDif = 0.3489773888652304 Gradient Norm = 216.8582055399408 Tiempo : 3.203 segundos
Logit model iteration(4) LogLikelyhood = -1.#INF maxAbsDif = 0.2252448891341937 Gradient Norm = 132.5871946500478 Tiempo : 3.188 segundos
Logit model iteration(5) LogLikelyhood = -1.#INF maxAbsDif = 0.2184098783931245 Gradient Norm = 259.0016938189552 Tiempo : 3.219 segundos
Logit model iteration(6) LogLikelyhood = -1.#INF maxAbsDif = 0.2141270332939203 Gradient Norm = 121.1500781359608 Tiempo : 3.187 segundos
Logit model iteration(7) LogLikelyhood = -1.#INF maxAbsDif = 0.2207307660479224 Gradient Norm = 245.4682477045687 Tiempo : 3.188 segundos
Logit model iteration(8) LogLikelyhood = -1.#INF maxAbsDif = 0.2228390613032262 Gradient Norm = 126.2880420563238 Tiempo : 3.203 segundos
Logit model iteration(9) LogLikelyhood = -1.#INF maxAbsDif = 0.2206495929879774 Gradient Norm = 251.8340661491895 Tiempo : 3.187 segundos
Logit model iteration(10) LogLikelyhood = -1.#INF maxAbsDif = 0.2198199000609777 Gradient Norm = 124.334223060156 Tiempo : 3.188 segundos
Logit model iteration(11) LogLikelyhood = -1.#INF maxAbsDif = 0.2206232593937018 Gradient Norm = 249.3775824242171 Tiempo : 3.187 segundos
Logit model iteration(12) LogLikelyhood = -1.#INF maxAbsDif = 0.2209297922887828 Gradient Norm = 125.0626477692595 Tiempo : 3.188 segundos
Logit model iteration(13) LogLikelyhood = -1.#INF maxAbsDif = 0.2206346758654199 Gradient Norm = 250.2820060063693 Tiempo : 3.187 segundos
Logit model iteration(14) LogLikelyhood = -1.#INF maxAbsDif = 0.2205214630883892 Gradient Norm = 124.7942732376469 Tiempo : 3.188 segundos
Logit model iteration(15) LogLikelyhood = -1.#INF maxAbsDif = 0.2206319101317311 Gradient Norm = 249.9471168674323 Tiempo : 3.187 segundos
Logit model iteration(16) LogLikelyhood = -1.#INF maxAbsDif = 0.2206740088087957 Gradient Norm = 124.8941738699272 Tiempo : 3.172 segundos
Logit model iteration(17) LogLikelyhood = -1.#INF maxAbsDif = 0.2206333171968811 Gradient Norm = 250.071515078183 Tiempo : 3.203 segundos
Logit model iteration(18) LogLikelyhood = -1.#INF maxAbsDif = 0.2206177384352029 Gradient Norm = 124.8572213844049 Tiempo : 3.172 segundos
Logit model iteration(19) LogLikelyhood = -1.#INF maxAbsDif = 0.2206328904031953 Gradient Norm = 250.0254568955057 Tiempo : 3.188 segundos
Logit model iteration(20) LogLikelyhood = -1.#INF maxAbsDif = 0.2206386745022871 Gradient Norm = 124.8709437231808 Tiempo : 3.187 segundos
Logit model iteration(21) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330715390124 Gradient Norm = 250.0425526818025 Tiempo : 3.188 segundos
Logit model iteration(22) LogLikelyhood = -1.#INF maxAbsDif = 0.2206309286696235 Gradient Norm = 124.8658603693529 Tiempo : 3.203 segundos
Logit model iteration(23) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330098066635 Gradient Norm = 250.0362181234874 Tiempo : 3.187 segundos
Logit model iteration(24) LogLikelyhood = -1.#INF maxAbsDif = 0.2206338047973039 Gradient Norm = 124.8677463415578 Tiempo : 3.203 segundos
Logit model iteration(25) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330339733627 Gradient Norm = 250.0385679920904 Tiempo : 3.188 segundos
Logit model iteration(26) LogLikelyhood = -1.#INF maxAbsDif = 0.2206327392986489 Gradient Norm = 124.8670472946448 Tiempo : 3.187 segundos
Logit model iteration(27) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330253111616 Gradient Norm = 250.0376969327074 Tiempo : 3.188 segundos
Logit model iteration(28) LogLikelyhood = -1.#INF maxAbsDif = 0.2206331345978415 Gradient Norm = 124.8673065550081 Tiempo : 3.172 segundos
Logit model iteration(29) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330285926491 Gradient Norm = 250.0380199739106 Tiempo : 3.187 segundos
Logit model iteration(30) LogLikelyhood = -1.#INF maxAbsDif = 0.2206329880755525 Gradient Norm = 124.8672104371507 Tiempo : 3.188 segundos
Logit model iteration(31) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330273921058 Gradient Norm = 250.0379002067471 Tiempo : 3.187 segundos
Logit model iteration(32) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330424167947 Gradient Norm = 124.8672460800733 Tiempo : 3.188 segundos
Logit model iteration(33) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330278410212 Gradient Norm = 250.0379446186832 Tiempo : 3.187 segundos
Logit model iteration(34) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330222702808 Gradient Norm = 124.8672328647088 Tiempo : 3.172 segundos
Logit model iteration(35) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330276754356 Gradient Norm = 250.0379281518504 Tiempo : 3.203 segundos
Logit model iteration(36) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330297410974 Gradient Norm = 124.8672377650314 Tiempo : 3.203 segundos
Logit model iteration(37) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330277370313 Gradient Norm = 250.037934257792 Tiempo : 3.204 segundos
Logit model iteration(38) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330269711192 Gradient Norm = 124.8672359480712 Tiempo : 3.187 segundos
Logit model iteration(39) LogLikelyhood = -1.#INF maxAbsDif = 0.2206330277142518 Gradient Norm = 250.0379319938005 Tiempo : 3.172 segundos
Probability calculation for each case i.e:
Matrix p = Exp(X*)$/RSum(Exp(X*B),1);
where X is the input matrix of Logit regression and B is the result parameter matrix is quite different to the probability calculated in the results of Logit function.
I have a private example that I will send to you.
Change History (6)
comment:1 Changed 17 years ago by
comment:2 Changed 17 years ago by
| Status: | new → assigned |
|---|
We are working about this problem
Thanks for reporting
comment:3 Changed 17 years ago by
There was two independent problems
Logarithm of likelihood becomes -Inf
Formulae for scalar logarithm of likelihood in each point can be expressed as
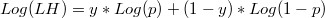
where p can be calculated from these two alternative formulaes that can originate numeric problems in some circumstances
- Positive way:
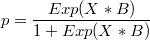
When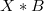 is a too large positive number
is a too large positive number 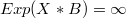 ,
, 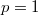 and
and 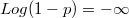
- Negative way:

When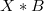 is a too large negative number
is a too large negative number 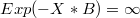 ,
, 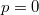 and
and 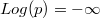
To solve these problems we can use these formulaes
- When
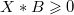 :
:
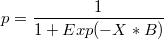
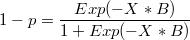
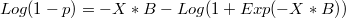
- When
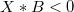 :
:
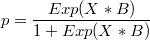
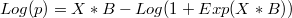
Values of p and B are incongruent
After each iteration values of B are updated by solution of linear differenced problem. So after the last iteration, values of p and other items were refered to values of B at previous iteration. When series converges to a unique point, difference between two iterations tends to zero, and this problem is almost invisible. But in your case the series has two points of convergency Gradient Norm = 124.8672359480712 and the other one around Gradient Norm = 250.0379319938005 . So, the difference becomes significative between consecutive iterations.
comment:4 Changed 17 years ago by
| Resolution: | → fixed |
|---|---|
| Status: | assigned → closed |
comment:6 Changed 17 years ago by
| Milestone: | → Manteinance |
|---|

It's possible that in other cases when appear LogLikelyhood? = -1.#INF in log, the function works well. But I think that we have test that probability is calculated correctly.