close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Opened 15 years ago

Closed 15 years ago

#789 closed task (fixed)

Multiple-try Metropolis

Reported by: Víctor de Buen Remiro Owned by: Víctor de Buen Remiro
Priority: highest Milestone: Numerical methods
Component: Math Version:
Severity: blocker Keywords:
Cc:

Description (last modified by Víctor de Buen Remiro)

Habría que explorar las posibles ventajas del método MCMC descrito en ​http://en.wikipedia.org/wiki/Multiple-try_Metropolis

Es una generalización del Metropolis-hastings que consiste básicamente en que en cada simulación se mezclan muchos candidatos, que es lo rápido de calcular, para conseguir candidatos mejores y que el ratio de aceptación sea mayor y así hacer menos simulaciones.

Definición de las funciones usadas en la simulación de ensayo múltiple de Metropolis-Hastings

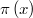  • \pi\left(x\right) : la función de densidad objetivo
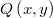  • Q\left(x,y\right) : la función de densidad del generador de candidatos que debe cumplir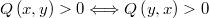 Q\left(x,y\right)>0\Longleftrightarrow Q\left(y,x\right)>0
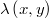  • \lambda\left(x,y\right) : una función simétrica no negativa, esto es,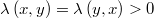 \lambda\left(x,y\right) = \lambda\left(y,x\right) >0
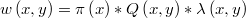  • w\left(x,y\right) = \pi\left(x\right) * Q\left(x,y\right) * \lambda\left(x,y\right) : la función de pesos

Algoritmo

  • Sea 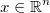x \in\mathbb{R}^{n} el punto actual de la cadena de Markov
  • Se toman 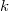k muestras independientes

\left\{ y_{j}\right\} _{j=1\ldots k} generadas con densidad Q\left(x,y_j\right)

  • Se selecciona aleatoriamente una de ellas de forma proporcional a sus pesos 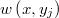w\left(x,y_j\right) , a la que llamaremos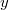 y
  • Se genera el conjunto de referencia como 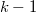k-1 muestras independientes

\left\{ x_{j}\right\} _{j=1\ldots k-1} generadas con densidad Q\left(y,x_j\right) y se toma x_k = x

  • Finalmente se acepta el candidato 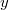y con probabilidad


r= \min \left( 1, \frac{\overset{k}{\underset{j=1}{\sum}}w\left(x,y_{j}\right)}{\overset{k}{\underset{j=1}{\sum}}w\left(x_{j},y\right)} \right)


Quizás habría que programarlo en C++ para que sea más eficiente, pero con una API centrada en efectuar una simulación aislada de un solo bloque, pasándole todos los argumentos necesarios cada vez, pues de esta manera es trivial enmarcarlo dentro de un proceso de simulación por bloques de MH o de Gibbs como BSR o cualquier otro posible. En esas tareas logísticas no es donde se gasta el tiempo de los simuladores y pueden estar perfectamente escritos en TOL como el propio BSR.

Change History (4)

comment:1 Changed 15 years ago by Víctor de Buen Remiro

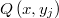
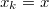
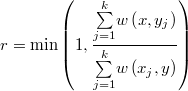
En el ticket #890 se expone una especialización para una familia concreta de problemas:

  • El método Multiple-try Metropolis de simulación de cadenas de Markov sobre densidades unimodales con dominios acotados arbitrariamente

comment:2 Changed 15 years ago by Víctor de Buen Remiro

Description: modified (diff)

comment:3 Changed 15 years ago by Víctor de Buen Remiro

Description: modified (diff)

comment:4 Changed 15 years ago by Víctor de Buen Remiro

Resolution: → fixed
Status: new → closed

(In [2218]) Fixes #789

Note: See TracTickets for help on using tickets.