Opened 16 years ago
Last modified 15 years ago
#890 closed task
El método Multiple-try Metropolis de simulación de cadenas de Markov sobre densidades unimodales con dominios acotados arbitrariamente — at Version 1
| Reported by: | Víctor de Buen Remiro | Owned by: | Víctor de Buen Remiro |
|---|---|---|---|
| Priority: | highest | Milestone: | Numerical methods |
| Component: | BSR | Version: | head |
| Severity: | critical | Keywords: | |
| Cc: |
Description (last modified by )
El método de simulación de cadenas de Markov Multiple-try Metropolis ofrece muchas posibilidades de aceleración de la convergencia cuando se tiene una forma rápida de evaluar la función de densidad conjunta.
En el ticket #789 se propone el método general pero aquí nos ocuparemos de su aplicación en el caso de dominios acotados arbitrariamente, pues podría ser muy útil en el sistema BSR, especialmente para mejorar la eficiencia de la simulación del bloque ARMA o los bloques no lineales que actualmente se simulan escalarmente (con SLICE ó ARMS) con una gran sobrecarga de trabajo.
Concretamente, cuando se sabe que la función de densidad es unimodal, y se tiene una forma rápida de evaluar la pertenencia al dominio de un punto candidato arbitrario, es posible implementar una función de generación de candidatos independiente del punto de partida y multinormal, eventualmente truncada, que la aproxime. Para mayor eficiencia consideraremos incorrelada y más adelante nos ocuparemos de proponer el cálculo de sus parámetros
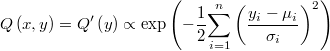
Cuando el dominio es acotado, la función generadora de candidatos está truncada en una región cuya expresión algebraica no es conocida, y aunque lo fuera, sería muy costoso calcular su integral de forma exacta. Por ello se debe calcular de forma aproximada, y la forma más sencilla de hacerlo es generar 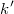 precandidatos hasta obtener
precandidatos hasta obtener 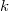 que estén dentro del dominio y podamos llamar candidatos. La función de densidad generadora de candidatos se podría aproximar como sigue:
que estén dentro del dominio y podamos llamar candidatos. La función de densidad generadora de candidatos se podría aproximar como sigue:
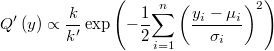
Tomando la función simétrica y positiva
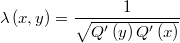
se obtiene la función de pesos
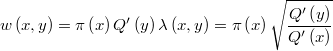
que resulta ser independiente del factor 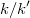 por lo que no tiene ninguna importancia si aproxima mejor o peor la integral de la densidad multinormal de precandidatos en el dominio. Esta es precisamente la razón por la que se toma una función de generación de candidatos independiente del punto de origen, en lugar de una simétrica que resulta más sencilla en el caso de dominio no acotado, pero que es inviable en el caso acotado cuando la moda se encuentra demasiado cerca de la frontera.
por lo que no tiene ninguna importancia si aproxima mejor o peor la integral de la densidad multinormal de precandidatos en el dominio. Esta es precisamente la razón por la que se toma una función de generación de candidatos independiente del punto de origen, en lugar de una simétrica que resulta más sencilla en el caso de dominio no acotado, pero que es inviable en el caso acotado cuando la moda se encuentra demasiado cerca de la frontera.
Para poder aplicar el método se comenzará tomando una media arbitraria 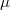 interior al dominio que puede ser perfectamente el propio punto inicial de la cadena y desviaciones unitarias
interior al dominio que puede ser perfectamente el propio punto inicial de la cadena y desviaciones unitarias 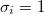 . Durante un número de iteraciones preliminares (burn-in) se irá desplazando la media al punto de mayor densidad objetivo de los
. Durante un número de iteraciones preliminares (burn-in) se irá desplazando la media al punto de mayor densidad objetivo de los 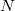 candidatos evaluados por el camino y las desviaciones se aproximarán como
candidatos evaluados por el camino y las desviaciones se aproximarán como
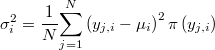
Durante la fase de simulación propiamente dicha se podría estudiar la revisión de estos parámetros si se observa un aumento excesivo de los rechazos.
Change History (1)
comment:1 Changed 16 years ago by
| Description: | modified (diff) |
|---|---|
| Summary: | El método Multiple-try Metropolis de simulación de cadenas de Markov → El método Multiple-try Metropolis de simulación de cadenas de Markov sobre densidades unimodales con dominios acotados arbitrariamente |
