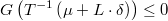close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

  1. Package BysDecision
    1. Definiciones
      1. Decisión binaria
      2. Decisión continua
      3. Decisión biunívoca
      4. Decisión con restricciones
        1. Combinación de previsiones

Package BysDecision

El paquete BysDecision ofrece utilidades relacionadas con problemas de decisión bayesiana en ambiente de incertidumbre.

Definiciones

Sea 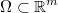\Omega \subset \mathbb{R}^{m} el espacio de todas las decisiones o acciones posibles que puede tomar un decisor.

Sea una variable aleatoria vectorial 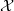\mathcal{X} con dominio 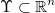\Upsilon\subset\mathbb{R}^{n} cuya distribución conjunta es conocida y que recoge todas las situaciones de las cuales no es posible tener un conocimiento determinista antes de tomar la decisión.

Para cada posible decisión 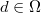d\in\Omega y cada posible situación 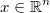x\in\mathbb{R}^{n} , es decir cada posible realización de 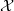\mathcal{X} , el coste de la acción para el decisor es una función real conocida

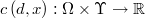
c\left(d,x\right):\Omega\times\Upsilon\rightarrow\mathbb{R}

Se pretende encontrar la decisión que minimiza la esperanza del coste

C\left(d\right)=E\left[c\left(d,\mathcal{X}\right)\right]

Nótese que en lugar de función de coste podría definirse una función de beneficio a maximizar sin más que multiplicarla por menos uno. Cuando el beneficio se mide en dinero hay que tener en cuenta que lo que importa en realidad es la utilidad de la riqueza para el decisor, que será una función cóncava para decisores aversos al riesgo, convexa para los amantes del riesgo y lineal para los neutros frente al riesgo.

Decisión binaria

Cuando sólo hay dos posibles acciones,

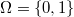
\Omega = \left\{ 0,1\right\}

hablaremos de decisión binaria o booleana.

Por ejemplo, un agricultor debe decidir si ir a regar un campo a manta o no hacerlo, pero no puede decidir qué cantidad de agua utilizar sino que ésta está fijada por el método de riego. El coste de la acción depende de que llueva o no y en qué medida lo haga:

  • Si decide regar y
    • no llueve de forma significativa el coste de la acción es nulo,
    • llueve de forma moderada pierde el tiempo y el combustible necesarios para desplazarse,
    • llueve de forma excesiva pierde además parte de la cosecha de forma proporcional al exceso de agua.
  • Si decide no regar y
    • no llueve de forma significativa pierde toda la cosecha
    • llueve de forma moderada el coste de la acción es nulo,
    • llueve de forma excesiva pierde parte de la cosecha de forma proporcional al exceso de agua.

La importancia de este tipo de problemas reside en que cualquier problema de decisión en el que haya un número finito de opciones cualitativas puede reformularse como un árbol de decisiones binarias.

Decisión continua

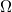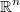Si el conjunto de decisiones \Omega tiene medida no nula en \mathbb{R}^{n} diremos que se trata de una decisión continua. Esto no implica necesariamente que la variable aleatoria sea continua.

Por conveniencia, también se aplicará esta etiqueta cuando el espacio de opciones sea discreto y ordenado y el número de opciones sea suficientemente grande para despreciar el efecto de la discretización. En tales casos la solución continua se discretizará por redondeo directo o probando las soluciones discretas más cercanas a la continua.

Por ejemplo, en las apuestas deportivas se puede decidir apostar cualquier cantidad de dinero entre 0 y el máximo disponible por el decisor y admitido por la casa de apuestas, mientras que el conjunto de resultados posibles suele ser finito y muy pequeño: {gana local,gana visitante}, {1,X,2}, etc.

Decisión biunívoca

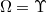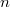Cuando cada posible decisión se puede asociar de forma biunívoca a cada posible situación, es decir, \Omega = \Upsilon , entonces diremos que se trata de decisión biunívoca. Un caso típico es la distribución de material perecedero para su venta entre un conjunto de n puntos de venta, en el que la demanda en cada punto de venta sería la variable aleatoria. Si se pone en servicio demasiado material en un punto dado, el exceso se perderá total o casi totalmente, si es posible reciclarlo en alguna medida, mientras que si se sirve poco se pierde el beneficio de la venta no realizada y se aumenta el riesgo de que la clientela se pase a la competencia. Tanto las decisiones posibles como las situaciones inciertas son en este caso

\Omega = \Upsilon = \left[0,\infty\right]^{n}

Cuando el dominio es continuo, este tipo de problemas pueden resolverse mediante técnicas de optimización muy eficaces y robustas, por lo que a veces es interesante convertir el problema al caso continuo.

El principal escollo suele ser la evaluación de la esperanza del coste que involucra una integral que puede no ser analíticamente resoluble o bien requerir demasiado tiempo de cálculo. En tales casos, lo mejor es simular una muestra suficientemente larga de realizaciones de la distribución conjunta, y simplemente calcular la media de las evaluaciones de la función de coste en cada una de esas realizaciones. Si se tiene un modelo bayesiano tipo MCMC ya está disponible esa muestra. En cambio, si lo que se tiene son estimaciones máximo-verosímiles, entonces hay que usar la distribución asintótica que se desprende de las mismas.

Decisión con restricciones

Supongamos que en el caso anterior existen restricciones, como por ejemplo que la suma de las cantidades distribuidas no pueda superar las existencias disponibles.

Ya no se puede hablar propiamente de decisión biunívoca pues el conjunto de decisiones es un subconjunto del de situaciones, pero también están disponibles las mismas o gran parte de las técnicas de optimización aplicables a esta clase de problemas añadiendo las restricciones al problema de optimización.

Combinación de previsiones

Un caso particular de decisión con restricciones, que resulta muy interesante para los analistas de datos estadísticos, es la mal llamada combinación de previsiones, refiriéndose al problema de obtener estadísticos de un conjunto de variables aletarorias que sean congruentes con ciertas restricciones, las cuales deben cumplir en realidad las propias variables aleatorias, y por ende cada una de sus realizaciones conjuntas, pero no necesariamente sus estadísticos centrales: media, mediana y moda.

Si las distribuciones son todas normales y las restricciones son todas lineales, la media cumplirá dichas restricciones, pero en cualquier otro caso esto no ocurrirá así, y no siempre se tiene presente este hecho.

Un ejemplo típico de esta situación es la presencia de una variable aleatoria (a la que llamaremos global) que es la suma de las demás y para la que existe un modelo log-normal(o cualquier otra no normal) con menos varianza que en el de las partes también log-normales. Si el modelo se estima por simulación y conjuntamente, obligando a que cada muestra cumpla las restricciones, podremos ver cómo las medias de las partes no suman exactamente la media del global. Si cada modelo se estima por su lado ni las realizaciones ni los estadísticos cumplirán las restricciones. En este caso sería posible combinar las variables originales para dar otras que cumplieran las restricciones, pero como ya se ha dicho, los estadísticos centrales no tendrían porqué cumplirlas.

Como en muchas ocasiones se confunde el concepto de previsión, que es una variable aleatoria, con alguno de sus estadísticos centrales, que son simples números, los clientes suelen exigir que esos números sean coherentes con ciertas restricciones que son incompatibles con seguir siendo dichos estadísticos.

El analista debe tomar una decisión que consiste en decirle al cliente que la previsión es cierto número aún a sabiendas de que la previsión es una variable aleatoria y que lo que le entrega no es una previsión ni un estadístico de la msima, sino una decisión que es posible optimizar.

Lo ideal en estos casos sería convencer al cliente para investigar cuál es su función de coste real y calcularla o aproximarla en la medida de lo posible, o bien inferirla directamente si el negocio es suficientemente conocido y transparente.

Si el cliente es refractario a estos conceptos y no hay forma de averiguarla sin su colaboración, el analista sería muy libre de buscar su propia función de coste, entendida como el grado de rechazo por parte del cliente de las "previsiones" entregadas, o mejor aún, estableciendo en el contrato de servicio el precio según cada tipo de error. Si se observa que al cliente le gusta que el sesgo sea simétrico pues se pone una función simétrica, etc.; si prefiere equivocarse un poco más al alza que a la baja pues se va probando con distintos coeficientes relativos; etc. En cierta manera esto sería una forma de sonsacarle al cliente la función de coste de una forma inconsciente, pues muchas veces él tiene la intuición de lo que es bueno o malo para su negocio, aunque no sepa o no quiera trasladarlo a una formulación matemática.

En ausencia de información, se suele maximizar la verosimilitud, que en el caso de residuos normales independientes y estandarizados, sería igual que minimizar la suma de cuadrados de los sesgos. En el ejemplo explicado anteriormente de las log-normales cuya suma debe dar otra log-normal, habría que transformar las variables para obtener residuos normales estandarizados e independientes, y sustituir en la ecuación de restricción la variable original por su expresión en términos de ellos. Esta situación es generalizable a cualquier tipo de restricciones de igualdad y/o desigualdad

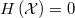
H\left(\mathcal{X}\right) = 0

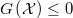
G\left(\mathcal{X}\right) \leq 0

sobre variables aleatorias transformadas de una multinormal mediante una función 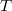T inversible

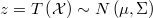
z=T\left(\mathcal{X}\right)\sim N\left(\mu,\Sigma\right)

Para estandarizar los residuos necesitamos de una descomposición simétrica de la matriz de covarianzas

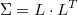
\Sigma=L\cdot L^{T}

que podría ser la de Cholesky si 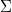\Sigma es definida positiva. De lo contrario habría que utilizar otra descomposición como la de valor singular para reducir las dimensiones de los residuos normales estandarizados e independientes al rango r de la matriz de covarianzas.

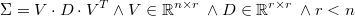
\Sigma=V \cdot D \cdot V^{T} \wedge V \in\mathbb{R}^{n \times r} \: \wedge D \in\mathbb{R}^{r \times r} \: \wedge r<n

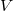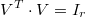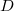donde V es ortonormal, es decir, V^{T} \cdot V = I_{r} , y D es diagonal con todos los valores diagonal estrictamente positivos.

La matriz de descomposición se puede definir entonces como

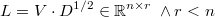
L = V \cdot D^{1/2} \in\mathbb{R}^{n \times r}\:\wedge r<n

En cualquier caso, los residuos normales estandarizados e independientes serían

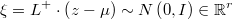
\xi=L^{+}\cdot\left(z-\mu\right)\sim N\left(0,I\right)\in\mathbb{R}^{r}

donde la pseudo-inversa de la matriz de descomposición simétrica sería

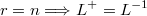
  • si r=n \Longrightarrow L^{+} = L^{-1}
  • si r<n \Longrightarrow L^{+} = D^{-1/2} \cdot V^{T}

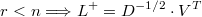
Siguiendo este criterio máximo-verosímil, la decisión óptima en la métrica transformada sería por tanto la solución del programa no lineal

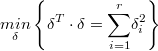
\underset{\delta}{min}\left\{ \delta^{T}\cdot\delta=\underset{i=1}{\overset{r}{\sum}}\delta_{i}^{2}\right\}

Sujeto a:

H\left(T^{-1}\left(\mu+L\cdot\delta\right)\right)=0

G\left(T^{-1}\left(\mu+L\cdot\delta\right)\right)\leq0

Para obtener la solución en términos originales bastaría con calcular

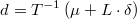
d=T^{-1}\left(\mu+L\cdot\delta\right)

Este cálculo es formalmente idéntico al de la decisión bayesiana óptima para la función de coste

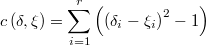
c\left(\delta,\xi\right)=\underset{i=1}{\overset{r}{\sum}}\left(\left(\delta_{i}-\xi_{i}\right)^{2}-1\right)

puesto que en tal caso la función a minimizar sería el coste esperado

C\left(\delta\right)=E\left[c\left(\delta,\mathcal{\xi}\right)\right]=E\left[\underset{i=1}{\overset{r}{\sum}}\left(\left(\delta_{i}-\xi_{i}\right)^{2}-1\right)\right]=\underset{i=1}{\overset{r}{\sum}}E\left[\delta_{i}^{2}-2\delta_{i}\xi_{i}+\xi_{i}^{2}-1\right]=\underset{i=1}{\overset{r}{\sum}}\left(\delta_{i}^{2}-2\delta_{i}E\left[\xi_{i}\right]+E\left[\xi_{i}^{2}\right]-1\right)

Sabemos por definición que

E\left[\xi_{i}\right]=0 \: \wedge \: E\left[\xi_{i}^{2}\right]=1

así que nos queda

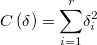
C\left(\delta\right)=\underset{i=1}{\overset{r}{\sum}}\delta_{i}^{2}

Como la constante aditiva es irrelevante, la función de coste equivalente podría ser igualmente

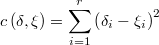
c\left(\delta,\xi\right)=\underset{i=1}{\overset{r}{\sum}}\left(\delta_{i}-\xi_{i}\right)^{2}

En la siguiente imagen se puede ver la gráfica del coste esperado para una normal unidimensional con funciones de coste cuadrática y valor absoluto:

source:/tolp/OfficialTolArchiveNetwork/BysDecision/doc/normal_expected_costs.PNG

Resulta evidente que ambas funciones de coste conducen a la misma decisión óptima con y sin restricciones, y la forma máximo-verosímil tiene la ventaja de ser el coste esperado analítico y con una expresión muy simple. Sin embargo hay que tener en cuenta que sólo se debe recurrir a este artificio si realmente no hay forma de acercarse a la función de coste real.

Una función de coste bastante habitual en los clientes es la del error absoluto

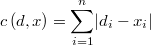
c\left(d,x\right)=\overset{n}{\underset{i=1}{\sum}}{\left|d_{i}-x_{i}\right|}

y también la del porcentaje de error absoluto

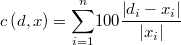
c\left(d,x\right)=\overset{n}{\underset{i=1}{\sum}}100\frac{\left|d_{i}-x_{i}\right|}{\left|x_{i}\right|}

En la siguiente gráfica se puede ver como en este caso pueden diverger bastante la solución máximo-verosímil y las decisiones bayesianas para estas dos funciones de coste. Se trata de una distribución log-normal bivariante correlada tal que la suma de las componentes debe sumar cierta constante. En el eje X se sitúa la primera coordenada de la decisión, la cual determina la segunda por completo.

source:/tolp/OfficialTolArchiveNetwork/BysDecision/doc/LogOfLikelihood_Vs_CostAverage.gif

Last modified 13 years ago Last modified on Sep 15, 2011, 8:22:20 AM