| Version 1 (modified by , 15 years ago) (diff) |
|---|
Post-procesado de cadenas de Markov
Los métodos tradicionales de post-procesado basados en el burn-in y el thinning son demasiado arbitrarios para poder parametrizarlos de forma automática sin intervención del usuario.
Las cadenas simuladas con BysSampler cuentan con una ventaja adicional al conocerse la log-likelihood de cada muestra, pues esto permite contrastarla directamente con la densidad local empírica de los puntos cercanos que han sido generados en sus cercanías.
En una cadena perfectamente muestreada el número de puntos generados en torno a un punto dado debería ser proporcional a la verosimilitud media alrededor de dicho punto. Esto permite diseñar un criterio completamente objetivo para eliminar puntos de zonas sobre-muestreadas y sustituirlos por puntos en otras zonas infra-muestreadas.
Una posibilidad sería utilizar el algoritmo KNN para encontrar los vecinos más próximos de cada punto de la muestra de tamaño 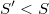 . Como en los métodos de simulación tipo accept-reject suele haber bastantes puntos repetidos, para que el algoritmo tenga sentido habría que tomar los
. Como en los métodos de simulación tipo accept-reject suele haber bastantes puntos repetidos, para que el algoritmo tenga sentido habría que tomar los 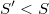 puntos únicos
puntos únicos
y llamar
al número de veces que aparece cada uno en la muestra. Obviamente, la suma de los números de apariciones da el tamaño muestral
Sean los 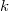 puntos muestrales vecinos de
puntos muestrales vecinos de 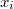 en orden de proximidad al mismo
en orden de proximidad al mismo
Sea la distancia euclídea del punto 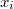 a su
a su 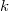 -ésimo vecino más próximo
-ésimo vecino más próximo
Así las cosas tenemos que el número total de puntos muestrales en la hiperesfera de radio 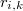 y centro
y centro 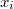 es
es
cantidad que se distribuye como una binomial
donde 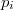 es la probabilidad de la hiperesfera, es decir, la integral de la función de densidad en esa hiperesfera
es la probabilidad de la hiperesfera, es decir, la integral de la función de densidad en esa hiperesfera
Esa integral sería algo muy costoso de evaluar, pero lo que sí conocemos sin coste adicional es el logaritmo de esa densidad, salvo una constante 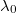 desconocida, evaluado en cada uno de los puntos muestrales, es decir, conocemos
desconocida, evaluado en cada uno de los puntos muestrales, es decir, conocemos
Podemos pues aproximar dicha integral como el producto de la media de las densidades por el hipervolumen de la región hiperesférica, que será proporcional a
obteniendo la relación
en la que 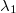 es una constante desconocida. Puesto que la probabilidad no puede ser mayor que 1 tenemos una cota de ella:
es una constante desconocida. Puesto que la probabilidad no puede ser mayor que 1 tenemos una cota de ella:
También es posible mejorar la aproximación de la integral por interpolación, concretamente mediante el método de Sheppard de ponderación inversa a la distancia que es muy eficiente pues no requiere de ninguna evaluación extra.
La probabilidad de que el número de puntos que caen dentro de la hiperesfera sea exactamente 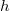 será por tanto
será por tanto
y el logaritmo de dicha probabilidad del contraste será
expresión en la cual se puede aproximar como.
Buscaremos el valor de 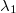 que maximiza la verosimilitud aproximada
que maximiza la verosimilitud aproximada
La probabilidad de que el número de puntos que caen dentro de la hiperesfera sea mayor o igual que 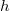 se calcula mediante la función beta incompleta
se calcula mediante la función beta incompleta

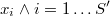
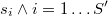
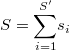
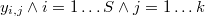
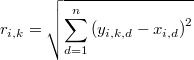
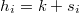
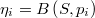
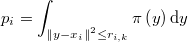
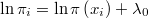
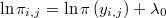
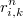
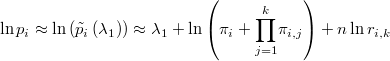
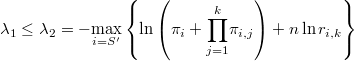
![P_i = \mathrm{Pr}\left[\eta_{i}=h_{i}\right]=\left(\begin{array}{c}S\\h_{i}\end{array}\right)p_{i}^{h_{i}}\left(1-p_{i}\right)^{S-h_{i}}](../chrome/site/images/latex/5d1b68d3735d875b88efd989c29df9d7.png)
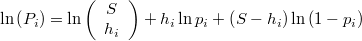
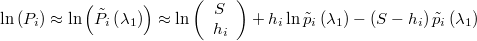
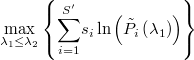
![\mathrm{Pr}\left[\eta_{i}\leq h_{i}\right]=I_{1-p}\left(S-h_{i},h_{i+1}\right)](../chrome/site/images/latex/5ef95b0de4915d6885f963e33749d8ef.png)