| Version 8 (modified by , 15 years ago) (diff) |
|---|
Post-procesado de cadenas de Markov
Introducción
Los métodos tradicionales de post-procesado de cadenas de simulación basados en el burn-in y el thinning son demasiado arbitrarios para poder parametrizarlos de forma automática sin intervención del usuario.
Las cadenas simuladas con BysSampler cuentan con una ventaja adicional al conocerse la log-likelihood de cada muestra, pues esto permite contrastarla directamente con la densidad local empírica de los puntos cercanos que han sido generados en sus cercanías.
En una cadena perfectamente muestreada el número de puntos generados en torno a un punto dado debería ser proporcional a la verosimilitud media alrededor de dicho punto. Esto permite diseñar un criterio completamente objetivo para eliminar puntos de zonas sobre-muestreadas e incluso sustituirlos por puntos en otras zonas infra-muestreadas.
Diseño de entornos locales solapados
El método propuesto será utilizar el algoritmo KNN que está disponible dentro del paquete TOL MatQuery, para encontrar los vecinos más próximos de cada punto de la muestra de tamaño 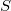 . Como en los métodos de simulación tipo accept-reject hay por definición puntos repetidos, para que el algoritmo tenga sentido habría que tomar los
. Como en los métodos de simulación tipo accept-reject hay por definición puntos repetidos, para que el algoritmo tenga sentido habría que tomar los 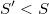 puntos únicos
puntos únicos
y llamar
al número de veces que aparece cada uno en la muestra. Obviamente, la suma de los números de apariciones da el tamaño muestral
Sean los 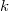 puntos muestrales vecinos de
puntos muestrales vecinos de 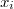 en orden de proximidad al mismo
en orden de proximidad al mismo
Sea la distancia euclídea del punto 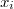 a su
a su 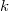 -ésimo vecino más próximo
-ésimo vecino más próximo
En cada punto muestral definiremos pues el entorno local como la hiperesfera de radio 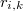 y centro
y centro 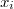
Distribución del cardinal local
Así las cosas tenemos que el cardinal local, es decir, el número total de puntos muestrales en 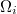 , es
, es
cantidad que se distribuye como una binomial
donde 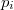 es la probabilidad de la hiperesfera, es decir, la integral de la función de densidad en cada entorno local
es la probabilidad de la hiperesfera, es decir, la integral de la función de densidad en cada entorno local
Aproximación de la probabilidad del entorno local
La anterior integral sería algo muy costoso de evaluar, pero lo que sí conocemos sin coste adicional es el logaritmo de la verosimilitud, salvo una constante 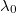 desconocida, evaluado en cada uno de los puntos muestrales, es decir, conocemos
desconocida, evaluado en cada uno de los puntos muestrales, es decir, conocemos
Podemos pues aproximar dicha integral por el método de Montecarlo, como el producto de la media de las verosimilitudes por el hipervolumen de la región hiperesférica, que será proporcional a
Es posible mejorar la aproximación de la integral por interpolación, concretamente mediante el método de Sheppard de ponderación inversa a la distancia que es muy eficiente pues no requiere de ninguna evaluación extra. Esto es especialemente recomendable si existen grandes diferencias en las verosimilitudes de los distintos puntos del vecindario. La interpolación será mejor realizarla en términos logarítmicos pues eso suavizará la función.
Para ello generaremos 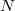 puntos con distribución uniforme en la hiperesfera
puntos con distribución uniforme en la hiperesfera
y calculamos la aproximación del logaritmo de la verosimilitud en cada uno de ellos mediante la fórmula de ponderación de Sheppard
De esta forma tenemos la fórmula de aproximación
en la que el error se postulará por comodidad normal, homocedástico e independiente
aunque cabría pensar que en los entornos de relieve más complicado el error puede ser mayor que en las zonas más suaves. Dicho de otra forma
con
Verosimilitud de los parámetros
La probabilidad de que el número de puntos que caen dentro de la hiperesfera sea exactamente 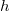 para la binomial definida anteriormente es
para la binomial definida anteriormente es
y el logaritmo de dicha probabilidad será
La verosimilitud de 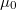 y
y 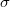 será la suma ponderada por las repeticiones del producto de la probabilidad anterior por la densidad del error de aproximación, luego la expresión de su logaritmo será
será la suma ponderada por las repeticiones del producto de la probabilidad anterior por la densidad del error de aproximación, luego la expresión de su logaritmo será
Como esta expresión depende de los errores de aproximación que no son contrastables habría que simularlos, lo cual podría resultar muy costoso, o bien aproximar la esperanza
Para ello se puede desarrollar para la función
la serie de Taylor de orden 2 centrada en 0
Si 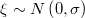 entonces la esperanza de esta función es aproximadamente
entonces la esperanza de esta función es aproximadamente
Como resulta que
su esperanza se puede aproximar como
es decir
Para que esta expresión sea evaluable debe cumplirse
Así pues tendremos el problema de optimización bivariante
Sujeto a
Test de super-población
La probabilidad de que el número de puntos que caen dentro de la hiperesfera sea mayor o igual que 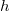 se calcula mediante la función beta incompleta
se calcula mediante la función beta incompleta

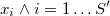
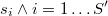
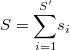
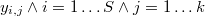
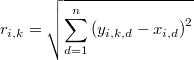
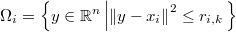
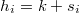
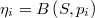
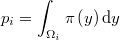
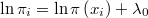
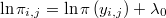
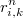
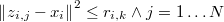
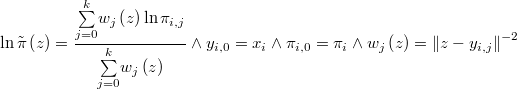
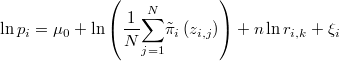
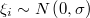
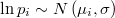
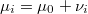
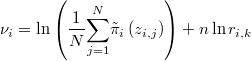
![P_i = \mathrm{Pr}\left[\eta_{i}=h_{i}\right]=\left(\begin{array}{c}S\\h_{i}\end{array}\right)p_{i}^{h_{i}}\left(1-p_{i}\right)^{S-h_{i}}](../chrome/site/images/latex/5d1b68d3735d875b88efd989c29df9d7.png)
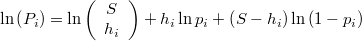
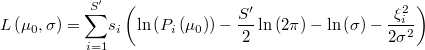
![E\left[L\left(\mu_0,\sigma\right)\right]=\underset{i=1}{\overset{S'}{\sum}}s_{i}\left(E\left[\ln\left(P_{i}\right)\right]-\frac{S'}{2}\ln\left(2\pi\right)-S'\ln\left(\sigma\right)-\frac{1}{2}S'\right)](../chrome/site/images/latex/cb409f30caa104efaac40dfc6e0b7766.png)
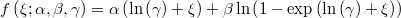
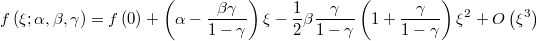
![E\left[f\left(\xi;\alpha,\beta,\gamma\right)\right]\approx f\left(0\right)-\frac{1}{2}\frac{\gamma}{1-\gamma}\left(1+\frac{\gamma}{1-\gamma}\right)\beta\sigma^{2}](../chrome/site/images/latex/77922ee2f97ac7fb13798ad43df72666.png)
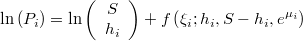
![E\left[\ln\left(P_{i}\right)\right]\approx\ln\left(\begin{array}{c}S\\h_{i}\end{array}\right)+E\left[f\left(\xi_i;h_{i},S-h_{i},e^{\mu_{i}}\right)\right]](../chrome/site/images/latex/d8d24defda44146dd6bba43f154e3603.png)
![E\left[\ln\left(P_{i}\right)\right]\approx\ln\left(\begin{array}{c}S\\h_{i}\end{array}\right)+h_{i}\mu_{i}+\left(S-h_{i}\right)\ln\left(1-e^{\mu_{i}}\right)-\frac{1}{2}\frac{e^{\mu_{i}}}{1-e^{\mu_{i}}}\left(1+\frac{e^{\mu_{i}}}{1-e^{\mu_{i}}}\right)\left(S-h_{i}\right)\sigma^{2}](../chrome/site/images/latex/19752e79d1d291217fda8a8e9c940f45.png)
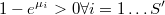
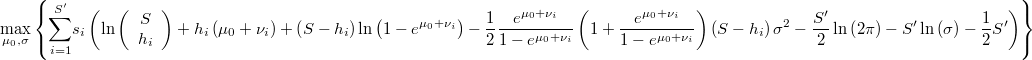
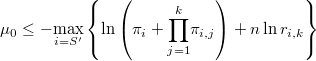
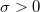
![\mathrm{Pr}\left[\eta_{i}\leq h_{i}\right]=I_{1-p}\left(S-h_{i},h_{i+1}\right)](../chrome/site/images/latex/5ef95b0de4915d6885f963e33749d8ef.png)