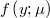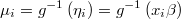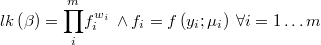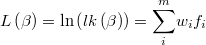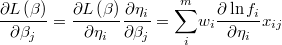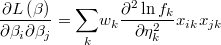wiki:OfficialTolArchiveNetworkGrzLinModel

Context Navigation

close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Package GrzLinModel
1. Weighted Generalized Regresions

Package GrzLinModel

Max-likelihood and bayesian estimation of generalized linear models with prior information and constraining linear inequations.

Weighted Generalized Regresions

Abstract class GrzLinModel::@WgtReg is the base to inherit weighted generalized linear regressions as poisson, binomial, normal or any other, given just the scalar link function 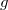$g$ and the density function $f$ .

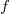In a weighted regression each row of input data has a distinct weight in the likelihood function. For example, it can be very usefull to handle with data extrated from an stratified sample.

Let be

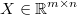$X\in\mathbb{R}^{m\times n}$ the regression input matrix
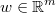$w\in\mathbb{R}^{m}$ the vector of weights of each register
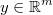$y\in\mathbb{R}^{m}$ the regression output matrix
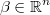$\beta\in\mathbb{R}^{n}$ the regression coefficients
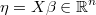$\eta=X\beta\in\mathbb{R}^{n}$ the linear prediction
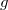$g$ the link function
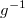$g^{-1}$ the inverse-link or mean function
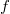$f$ the density function of a distribution of the exponential family

Then we purpose that the average of the output is the inverse of the link function applyied to the linear predictor

$E\left[y\right]=\mu=g^{-1}\left(X\beta\right)$

The density function becomes as a real valuated function of at least two parameters

$f\left(y;\mu\right)$

For each row 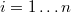$i=1 \dots n$ we will know the output 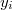$y_i$ and the average

$\mu_i=g^{-1}\left(\eta_i\right)=g^{-1}\left(x_i\beta\right)$

Each particular distribution may have its own additional parameters which will be treated as a different Gibbs block and should implement next methods in order to be able of build both bayesian and max-likelihood estimations

the mean function:

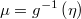
$\mu = g^{-1}\left(\eta\right)$
the log-density function:

$\ln f$
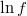
the first and second partial derivatives of log-density function respect to the linear prediction

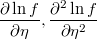
$\frac{\partial\ln f}{\partial\eta},\frac{\partial^{2}\ln f}{\partial\eta^{2}}$

The likelihood function of the weigthed regression is then

$lk\left(\beta\right)=\overset{m}{\underset{i}{\prod}}f_{i}^{w_{i}}\:\wedge f_{i}=f\left(y_{i};\mu_{i}\right)\:\forall i=1\ldots m$

and its logarithm

$L\left(\beta\right)=\ln\left(lk\left(\beta\right)\right)=\overset{m}{\underset{i}{\sum}}w_{i}f_{i}$

The gradient of the logarithm of the likelihood function will be

$\frac{\partial L\left(\beta\right)}{\partial\beta_{j}}=\frac{\partial L\left(\beta\right)}{\partial\eta_{i}}\frac{\partial\eta_{i}}{\partial\beta_{j}}=\overset{m}{\underset{i}{\sum}}w_{i}\frac{\partial\ln f_{i}}{\partial\eta_{i}}x_{ij}$

and the hessian is

$\frac{\partial L\left(\beta\right)}{\partial\beta_{i}\partial\beta_{j}}=\underset{k}{\sum}w_{k}\frac{\partial^{2}\ln f_{k}}{\partial\eta_{k}^{2}}x_{ik}x_{jk}$

This class also implements these common features extending the generalized linear model class:

linear constraining inequations over linear parameters

$A \beta \ge a$
scalar prior information of type normal or uniform, truncated or not in both cases,

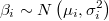
$\beta_i \sim N\left(\mu_{i},\sigma^2_{i}\right)$

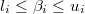
$l_i \le \beta_i \le u_i$
vectorial normal prior information (not implemented)

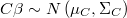
$C\beta \sim N\left(\mu_{C},\Sigma_{C}\right)$

Weighted Poisson Regresion

It will be implemented in GrzLinModel::@WgtPoisson but is not available yet. There is an example of use in test_0002/test.tol

In this case we have

the link function

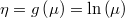
$\eta = g\left(\mu\right)=\ln\left(\mu\right)$
the mean function

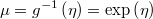
$\mu = g^{-1}\left(\eta\right)=\exp\left(\eta\right)$
the probability mass function

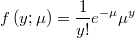
$f\left(y;\mu\right)=\frac{1}{y!}e^{-\mu}\mu^{y}$
and its logarithm will be

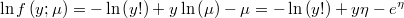
$\ln f\left(y;\mu\right)=-\ln\left(y!\right)+y\ln\left(\mu\right)-\mu = -\ln\left(y!\right)+y\eta-e^{\eta}$
the partial derivatives of log-density function respect to the linear prediction is

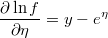
$\frac{\partial\ln f}{\partial\eta}=y-e^{\eta}$

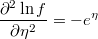
$\frac{\partial^{2}\ln f}{\partial\eta^{2}}=-e^{\eta}$

Weighted Qualitative Regresion

For boolean and qualitative response outputs like logit or probit there is an specialization on package QltvRespModel

Extended Regressions

Under certain circumstances, the optimization and simulation methods used over pure exponential family, can be extended to distributions with extra parameters than average.

This extra parameters can be simulated in a Gibbs frame by simple alternating and incorporating prior information about all them. In MLE optimization we can use Expectation–maximization algorithm to take profit of reusing written code.

Weighted Normal Regresion

Is implemented in GrzLinModel::@WgtNormal There is an example of use in test_0001/test.tol

In this case we have

the identity as link function and mean function

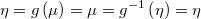
$\eta = g\left(\mu\right)= \mu = g^{-1}\left(\eta\right) = \eta$
the density function has the variance as extra parameter

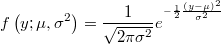
$f\left(y;\mu,\sigma^{2}\right)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{^{-\frac{1}{2}\frac{\left(y-\mu\right)^{2}}{\sigma^{2}}}}$
we can stablish an optional inverse chi-square prior over the variance or even fix it as a known value.
the log-density function will be

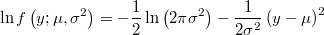
$\ln f\left(y;\mu,\sigma^{2}\right)= -\frac{1}{2}\ln\left(2\pi\sigma^{2}\right)-\frac{1}{2\sigma^{2}}\left(y}-\mu\right)^{2}$
the partial derivatives of log-density function respect to the linear prediction is

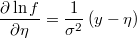
$\frac{\partial\ln f}{\partial\eta}=\frac{1}{\sigma^{2}}\left(y-\eta\right)$

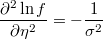
$\frac{\partial^{2}\ln f}{\partial\eta^{2}}=-\frac{1}{\sigma^{2}}$

Weighted Zero-Inflated Poisson Regresion

Is implemented in GrzLinModel::@WgtPoisson.ZeroInflated There is an example of use in test_0004/test.tol

This a mixture of Bernouilli and Poisson that inflates the probability of zero occurrences in a certain value

$\lambda\in\left[0,1\right]$

that will be called zero inflation and will be an extra parameter used to fit overdispersion.

When 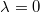$\lambda=0$ we have a Poisson and when 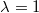$\lambda=1$ it's a Bernouilli.

the link function is the same than Poisson one

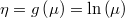
$\eta = g\left(\mu\right)=\ln\left(\mu\right)$

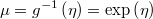
$\mu = g^{-1}\left(\eta\right)=\exp\left(\eta\right)$
the probability mass function is

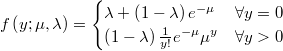
$f\left(y;\mu,\lambda\right)=\begin{cases}\lambda+\left(1-\lambda\right)e^{-\mu} & \forall y=0\\\left(1-\lambda\right)\frac{1}{y!}e^{-\mu}\mu^{y} & \forall y>0\end{cases}$
and its logarithm will be

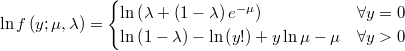
$\ln f\left(y;\mu,\lambda\right)=\begin{cases}\ln\left(\lambda+\left(1-\lambda\right)e^{-\mu}\right) & \forall y=0\\\ln\left(1-\lambda\right)-\ln\left(y!\right)+y\ln\mu-\mu & \forall y>0\end{cases}$
the first and second partial derivatives of log-density function respect to the linear prediction are

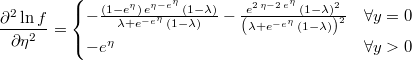
$\frac{\partial^{2}\ln f}{\partial\eta^{2}}=\begin{cases}-\frac{\left(1-{e}^{\eta}\right)\,{e}^{\eta-{e}^{\eta}}\,\left(1-\lambda\right)}{\lambda+{e}^{-{e}^{\eta}}\,\left(1-\lambda\right)}-\frac{{e}^{2\,\eta-2\,{e}^{\eta}}\,{\left(1-\lambda\right)}^{2}}{{\left(\lambda+{e}^{-{e}^{\eta}}\,\left(1-\lambda\right)\right)}^{2}} & \forall y=0\\-e^{\eta} & \forall y>0\end{cases}$
the first partial derivative of log-density function respect to the zero-inflation parameter is

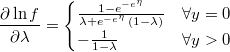
$\frac{\partial\ln f}{\partial\lambda}=\begin{cases}\frac{1-{e}^{-{e}^{\eta}}}{\lambda+{e}^{-{e}^{\eta}}\,\left(1-\lambda\right)} & \forall y=0\\-\frac{1}{1-\lambda} & \forall y>0\end{cases}$

Last modified 13 years ago Last modified on Feb 21, 2012, 8:37:45 PM

Download in other formats:

Plain Text