close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Version 1 (modified by Víctor de Buen Remiro, 14 years ago) (diff)

--

  1. Package GrzLinModel
    1. Weighted Generalized Regresions

Package GrzLinModel

Max-likelihood and bayesian estimation of ​generalized linear models.

Weighted Generalized Regresions

Abstract class @WgtReg is the base to inherit weighted generalized linear regressions as poisson, binomial, logit, probit or any other, given just the scalar distribution function 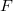F and the corresponding density function 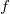f . In a weighted regression each row of input data has a distinct weight in the likelihood function. For example, it can be very usefull to handle with data extrated from an stratified sample.

Let be

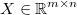  • X\in\mathbb{R}^{m\times n} the regression input matrix
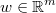  • w\in\mathbb{R}^{m} the vector of weights of each register
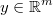  • y\in\mathbb{R}^{m} the regression output matrix
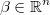  • \beta\in\mathbb{R}^{n} the regression coefficients
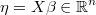  • \eta=X\beta\in\mathbb{R}^{n} the linear prediction
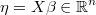  • \eta=X\beta\in\mathbb{R}^{n} the linear prediction
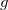  • g the link function
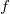  • f the density fuciton of a distribution of the

​exponential family

Then we purpose that the average of the output is the inverse of the link function applyied to the linear predictor

E\left[y\right]=\mu=g^{-1}\left(X\beta\right)