Simulación bayesiana con Metropolis within Gibbs

Introducción

Supongamos que queremos simular una variable aleatoria vectorial 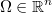cuya función de log-verosimilitud salvo constante es

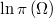
Si es posible evaluar esta función de forma eficiente el método Metropolis-Hastings o cualqueira de sus derivados nos permite simular una cadena de Markov de la distribución de .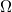

Si es demasiado compleja como para expresarse de forma analítica o bien es demasiado pesada de calcular entonces hay que tratar de dividir esta variable en bloques

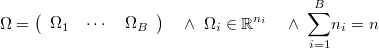
Si se conoce un método eficaz para simular cada bloque condicionado al resto entonces es aplicable el método de simulación de Gibbs por bloques.

Normalmente resulta mucho más sencillo evaluar la función de log-verosimilitud salvo constante condicionada al resto de bloques,

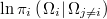
lo cual permite aplicar el método Metropolis Within Gibbs, que consiste en simular alternativamente los distintos bloques con el método de Metropolis-Hastigs (MH) o alguno similar como el Multiple Try Metroplis (MTM), dejando invariantes todos aquellos de los que depende. En cada simulación es necesario evaluar la log-verosimilitud un número de veces dependiente del método usado.

Este esquema tiene la ventaja de que sirve para simular cualquier clase de modelos implementando bloques de simulación para cada tipo de elemento que intervenga y definiendo aparte las relaciones de condicionamiento como meras reglas de asignación total o parcial de miembros de un bloque condicionado en función de los miembros del bloque condicionante.

Si para un bloque concreto se dispone de un método de generación condicionada que resulte más sencillo o eficaz que el MH o sus derivados, es perfectamente lícito aplicarlo siempre y cuando se respeten las relaciones de condicionamiento.

Arquitectura del sistema

Definiremos modelo de forma abstracta como un conjunto de bloques de variables aleatorias relacionados entre sí por mecanismos de condicionamiento que se ejecutan tras cada simulación de uno de ellos, para forzar así que la función de log-verosimilitud devuelva siempre los valores condicionados al resto de bloques.

El esquema planteado supondría la existencia de un objeto master que tuviera un listado de objetos bloque del modelo, que se irían añadiendo con mecanismos de ensamblaje que indicarían cómo un bloque condiciona a los ya existentes y cómo es condicionado por ellos según corresponda.

En lugar de tratar de programar un mini-lenguaje ad-hoc como se hizo en BSR, la idea es que se dote al sistema de una familia de clases en TOL que permitan crear declarativamente bloques primarios que implementen las distribuciones básicas más usuales, y de otra familia que permita relacionar bloques entre sí de forma algebraica para que queden perfectamente definidos los condicionamientos correspondientes.

Paralelización de procesos

Cuando un modelo es muy complejo, tiene demasiados bloques, o éstos tienen muchas variables, o de una u otra forma involucran el manejo de grandes cantidades de información, los modelos se hacen inmanejables si se pretende hacerlo en una computadora individual. Puede ser que no haya memoria suficiente o que aún habiéndola la velocidad de cálculo sea muy inferior a la requerida, con lo que es necesario paralelizar los procesos en diferentes máquinas para acomoter el problema.

Merece la pena puntualizar que se puede simular simultáneamente en paralelo aquellos bloques que no dependen entre sí, pero los que son interdependientes deben simularse secuencialmente para que las reglas de condicionamiento sean válidas. Para ello el máster del simulador debe conocer qué bloques condicionan a qué otros para establecer un grafo topológico de la red que forman y determinar en qué partes es posible paralelizar. No necesita saber cómo se relacionan los bloques entre sí ni cómo se implementan los condicionamientos, sino sólo entre qué bloques se dan y en qué sentido o sentidos, pues el condicionamiento puede ser unidireccional o bidireccional.

En la imagen de la derecha se presenta un caso muy simple pero bastante habitual de modelo en el que se observan

• una serie de bloques 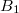a 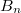están relacionados entre sí por lo que deben ser ejecutados secuencialmente.
• otro conjunto de bloques 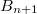a 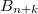independientes entre sí, que pueden por tanto ejecutarse en paralelo en distintas máquinas.
• una última serie de bloques 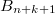a 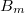dependientes entre sí, que deben ejecutarse secuencialmente.

Tras la simulación del último bloque se debe recolectar el estado actual de cada bloque como un vector fila que se concatena en el proceso maestro a los demás en el orden establecido, y después se vuelve al primero de los bloques para comenzar una nueva simulación, y así durante miles o hasta millones de veces.

Por este motivo es necesario que la transmisión de información que implica cada condicionamiento se realice de la forma más eficiente que sea posible, lo cual requiere un protocolo de comunicación adecuado cuando se establece un condicionamiento entre bloques manejados por distintas máquinas, como ocurre por ejemplo en los condicionamientos entre los bloques 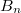y 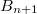o entre 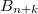y 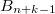del anterior diagrama.

Entidades básicas

Existen muchas formas de relación entre bloques. La acción a llevar a cabo para condicionar puede suponer desde modificar simplemente un valor escalar (como la sigma de un bloque de regresión lineal normal), hasta modificar total o parcialmente un valor vectorial o matricial, (como ocurre en el caso de los omitidos que deben trasladarse a un subconjunto arbitrariamente salteado de entre las celdas de la matriz de input o de output). Además, los valores con los que hay que sustituir los valores a condicionar no tienen porqué ser directamente los valores condicionadores, sino que en general serán el resultado de una función dependiente de los mismos. Por estos motivos no resulta ni mucho menos trivial condicionar de una forma genérica y eficiente.

Existen varias entidades en el sistema, algunas de las cuales darán lugar a una jerarquía de clases que permitirán adaptarse a todas las situaciones con una API mínima, mientras que otros conceptos son relativos al uso y no a su estructura por lo que no precisan de una clase

• @RandVar: Variable aleatoria generable mediante log-verosimilitud, sin perjuicio de que pueda haber otro método de generación alternativo más eficaz en alguna clase heredada.
• @Relation: Relación entre un bloque condicionante y otro condicionado que especifica sin ambigüedad posible todas las acciones a realizar.
• @Model: Conjunto de bloques de variables aleatorias y de relaciones de condicioanmiento. Es un tipo especial de variale aleatoria, por lo que hereda de @RandVar.
• Bloque: Variable aleatoria cuyo generador es llamado por un modelo según una estrategia de ejecución. de algún modo compatible con el algoritmo de Gibbs. Un modelo puede funcionar como un bloque de otro modelo.
• Estrategia: Forma de alternar o simultanear la simulación de los distintos bloques de Gibbs, de forma compatible con la estructura de relaciones.
• Master: Modelo principal formado por bloques que pueden ser a su vez modelos y que lanza las simulaciones de cada uno de ellos según la estrategia seleccionada y la va almacenando en disco.

Clase @RandVar

A la clase base de la que derivan todos las variables aleatorias (v.a.) la llamaremos Class @RandVar, pues lo que se está planteando no es otra cosa que un mecanismo de gestión de variables aleatorias por la vía de la generación de simulaciones por uno u otro método.

No toda v.a. definida tiene porqué ser un bloque de Gibbs de un modelo. Muchas veces un bloque se puede definir mediante operaciones algebraicas de otras variables aleatorias las cuales no pertenecerán directamente al modelo sino indirectamente a través de uno de sus bloques. Otro tipo de v.a. de gran utilidad serán las que definan la información a priori relativa a un bloque o a un modelo, simplemente sumando su log-verosimilitud.

En este nivel raíz estará disponible una batería de algoritmos de generación MCMC basados en la log-verosimilitud exclusivamente y que sean capaces de autocalibrarse sin intervención del usuario, pues deben adecuarse a cualquier distribución que se quiera generar:

  //Generates a single sample by means of Metropolis-Hastings algorithm
  VMatrix draw.MH(Real numSim) { ... }
  //Generates a single sample by means of Multiple Try Metropolis algorithm
  VMatrix draw.MTM(Real numSim) { ... }
  ...

El argumento numSim indica el número de simulación actual y es meramente informativo, para generación de errores y para posibles actuaciones dependientes de ese valor, por ejemplo durante el periodo de burning.

  //Generates a single sample
  VMatrix draw(Real numSim) { draw.MH(numSim) }

El método por defecto será Metropolis-Hastings y podrá ser cambiado en las clases heredadas para las que exista otro método directo más eficaz de muestreo.

Cuando no existe dicho método directo la clase derivada final, ésta debe implementar obligatoriamente el método que devuelve el logaritmo de la verosimilitud para poder aplicar alguno de los métodos MCMC

  //Returns log-likelihood except a constant for a given a vector as defined by inherited class
  Real _log_likelihood(VMatrix x);

Se trata de un método privado porque en la clase raíz se implementará el método público

  //Returns log-likelihood except a constant for a given a vector
  Real log_likelihood(VMatrix x) { ... }

que hará las comprobaciones básicas pertinentes, llamará al método privado y efectuará otro tipo de tareas internas que se irán explicando más adelante.

El método toma siempre un vector definido como un objeto de tipo VMatrix aunque se espere un escalar, para simplificar la API. Las dimensiones del argumento tienen que ser compatibles con lo que espera el bloque y de lo contrario se mostrará un error y se devolverá omitido. Si se quiere pasar un escalar y tiene sentido hacerlo se puede llamar al método

  //Returns log-likelihood except a constant for a given a sample
  Real log_likelihood.S(Real x) { log_likelihood(Constant(1,1,x) };

Si el argumento está fuera del dominio la verosimilitud es cero y su logaritmo es 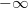. Todas las restricciones de igualdad o desigualdad, lineales o no, estarán reflejadas en el hecho de que se devolverá 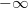cuando no se cumplan.

Variables aleatorias primarias

A los bloques primarios los llamaremos Primary Random Variable (PRV) y permiten tratar con variables aleatorias correspondientes a las distribuciones básicas que se requieran:

• Distribución determinista: @PRV.Cte::Create.V(VMatrix cte)
• Distribución uniforme continua: @PRV.UniCon::Create(Real size, Real from, Real until)
• Distribución uniforme discreta: @PRV.UniDis::Create(Real size, Real from, Real until)
• Distribución normal: @PRV.Normal::Create(Real size, Real nu, Real sigma)
• Distribución logística: @PRV.Logistic::Create(Real size, )
• Distribución de Bernouilli: @PRV.Bernouilli::Create(Real size, Real p)
• Distribución binomial: @PRV.Binomial::Create(Real size, Real p, Real k)
• Distribución de Poisson: @PRV.Poisson::Create(Real size, Real nu)
• Distribución t-student: @PRV.TStudent::Create(Real size, Real freDeg)
• Distribución chi-square: @PRV.ChiSquare::Create(Real size, Real freDeg)
• Distribución scaled inverse chi-square: @PRV.InvScaChiSquare::Create(Real size, Real freDeg, Real scale)
• ...

En todas aquellas para las que sea posible, que serán prácticamente todas, se dispondrá de un método especializado de generación directa de muestras sobrecargando el método draw

Variables aleatorias derivadas algebraicamente

A los bloques derivados algebraicamente los llamaremos Algebraic Derived Random Variable (RVOS) y permiten generar variables aleatorias que pueden ser muy complicadas de generar directamente, pero en cambio es trivial generarlas aplicando las operaciones sobre las generaciones de los argumentos.

Operaciones escalares

En este tipo de clases heredadas de @RandVar se puede aplicar operaciones aritméticas sobre instancias de @RandVar previamente creadas o bien sobre dichas instancias y valores escalares deterministas

• Suma:
  • @RVOS.Sum::Create(@RandVar a, @RandVar b),
  • @RVOS.Sum::Create.RV.S(@RandVar a, Real b),
  • @RVOS.Sum::Create.S.RV(Real a, @RandVar b)
• Resta:
  • @RVOS.Dif::Create(@RandVar a, @RandVar b),
  • @RVOS.Dif::Create.RV.S(@RandVar a, Real b),
  • @RVOS.Dif::Create.S.RV(Real a, @RandVar b)
• Producto:
  • @RVOS.Prod::Create(@RandVar a, @RandVar b),
  • @RVOS.Prod::Create.RV.S(@RandVar a, Real b),
  • @RVOS.Prod::Create.S.RV(Real a, @RandVar b)
• Cociente:
  • @RVOS.Div::Create(@RandVar a, @RandVar b),
  • @RVOS.Div::Create.RV.S(@RandVar a, Real b),
  • @RVOS.Div::Create.S.RV(Real a, @RandVar b)
• Potencia:
  • @RVOS.Power::Create(@RandVar a, @RandVar b),
  • @RVOS.Power::Create.RV.S(@RandVar a, Real b),
  • @RVOS.Power::Create.S.RV(Real a, @RandVar b)
• Transformación monaria: Aplica una función de R en R
  • @RVOS.Monary::Create(Code f, @RandVar a)
• Transformación binaria: Aplica una función de R^{2 en R}
  • @RVOS.Binary::Create(Code f, @RandVar a, @RandVar b)
  • @RVOS.Binary::Create.RV.S(Code f, @RandVar a, Real b),
  • @RVOS.Binary::Create.S.RV(Code f, Real a, @RandVar b)
• Transformación n-aria: Aplica una función de R^{n en R}
  • @RVOS.N_ary::Create(Code f, Set a)

En este tipo de operaciones resulta trivial simular llamando al simulador de las variables aleatorias involucradas y aplicando la operación sobre ellas. En cambio, si hay más de una variable aleatoria incvolucrada, el cálculo de la verosimilitud conlleva una integral numérica de alto coste computacional, por lo que el método devolverá omitido y no debe usarse.

Real _log_likelihood(VMatrix x) { ? }

Si se trata de una operación monaria o todos los argumentos son deterministas salvo uno entonces no hay ningún problema en calcular la verosimilitud aplicando primero la transformación inversa y llamando al método de la única v.a. propiamente dicha.

Operaciones matriciales

En este tipo de clases heredadas de @RandVar se puede aplicar operaciones aritméticas sobre instancias de @RandVar previamente creadas o bien sobre dichas instancias y valores vectoriales o matriciales deterministas

• Extracción:
  • Por índice: @RVOV.Extract.Cell::Create(@RandVar a, Set ij)
  • Por rango: @RVOV.Extract.Range::Create(@RandVar a, Real ini, Real num)
• Suma:
  • Post-Matricial: @RVOV.Sum.M.Post::Create(@RandVar a, VMatrix b),
  • Pre-Matricial: @RVOV.Sum.M.Pre::Create(VMatrix a, @RandVar b)
• Producto:
  • Post-Matricial: @RVOV.Prod.M.Post::Create(@RandVar a, VMatrix b),
  • Pre-Matricial: @RVOV.Prod.M.Pre::Create(VMatrix a, @RandVar b),
  • Celda a celda: @RVOV.Prod.M.Weighted::Create(@RandVar a, VMatrix b)
• Cholesky:
  • @RVOV.Chol.Prod::Create(VMatrix X, Text mode, @RandVar a): Aplica el factor de Cholesky de la matriz dada a una v.a. El argumento mode puede ser "X","XtX" ó "XXt" según se disponga de la matriz simétrica o de un factor suyo.
  • @RVOV.Chol.Solve.L::Create(VMatrix X, Text mode, @RandVar a): Resuelve el sistema L*b=a siendo L el factor de Cholesky de la matriz dada. El argumento mode puede ser "X","XtX" ó "XXt" según se disponga de la matriz simétrica o de un factor suyo.
  • @RVOV.Chol.Solve.Lt::Create(VMatrix X, Text mode, @RandVar a): Resuelve el sistema L'*b=a siendo L el factor de Cholesky de la matriz dada. El argumento mode puede ser "X","XtX" ó "XXt" según se disponga de la matriz simétrica o de un factor suyo.
  • @RVOV.Chol.Solve.LtL::Create(VMatrix X, Text mode, @RandVar a): Resuelve el sistema L'*L*b=a siendo L el factor de Cholesky de la matriz dada. El argumento mode puede ser "X","XtX" ó "XXt" según se disponga de la matriz simétrica o de un factor suyo.
  • @RVOV.Chol.Solve.LLt::Create(VMatrix X, Text mode, @RandVar a): Resuelve el sistema L*L'*b=a siendo L el factor de Cholesky de la matriz dada. El argumento mode puede ser "X","XtX" ó "XXt" según se disponga de la matriz simétrica o de un factor suyo.
• Regresor lineal: Y=X*b+e
  • @RVOV.LinReg::Create(VMatrix Y, VMatrix X, @RandVar e): Llama al log_likelihood de e con el resultado de Y-X*b
  • @RVOV.LinReg.Chol::Create(VMatrix Y, VMatrix X, @RandVar e) : Calcula directamente b = (X'X)^-1 X' (Y-e) Es útil cuando X es regular y constante y los residuos son normales de media 0, independientes y homocedásticos pues resulta muy eficaz en esos casos, especialmente si X es además sparse. Internamente se utiliza la descomposición de Cholesky.

Clase @Relation

Como ya se ha dicho la clase @Relation implementa una relación de condicionamiento entre un bloque de origen o condicionador y otro de destino o condicionado.

Relaciones de condicionamiento por asignación

En estos casos, cada bloque tiene su propia función de log-verosimilitud en la que alguno de sus elementos es una variable del otro, por lo que el condicionamiento se limita a que un bloque modifica en el otro lo que toque.

Relaciones de condicionamiento parasitario

Existe una amplia gama de filtros no lineales que modifican elementos como el output o el input de una regresión lineal. En todos ellos el bloque no lineal se limita a cambiar lo que toque del bloque de regresión, y su función de log-verosimilitud puede implementarse de forma parasitaria respecto a la de su anfitrión, llamándola cambiando no sus argumentos sino los miembros adecuados de la instancia.

Este tipo de relación entre bloques es extensible formalmente a todas las situaciones en las que hay un bloque anfitrión y otro parásito, cuya función de log-verosimilitud consistiría en modificar lo que toque dentro del bloque anfitrión y llamar a su función de log-verosimilitud sin modificar los argumentos. De esta forma el bloque anfitrión no tiene que realizar ninguna acción de condicionamiento específica sobre el bloque parásito, pues es inherente a la forma de cálculo. En este tipo de relación, las acciones necesarias para el condicionamiento y para la evaluación de la log-verosimilitud son exactamente las mismas.

En la clase raíz @RandVar se dispondrá de un miembro

  Set _.hosts = Copy(Empty);

para que los bloques parasitarios referencien a sus anfitriones

Clase @Model

Como ya se ha dicho un modelo es un conjunto de bloques y de relaciones de condicionamiento y es un caso paricular de variable aleatoria. Por lo tanto, un modelo puede ser un bloque de otro modelo y tener relaciones de condicionamiento con otros bloques que a su vez podrían ser modelos o bloques simples.

Llamaremos master al modelo raíz que no actúa como bloque de ningún otro y es el encargado de manejar todo el sisteam de simulación.

Un modelo se declara siempre vacío en primera instancia y después se le van añadiendo sus componentes de forma coherente, es decir, para poder añadir una relación entre dos bloques, estos deben haber sido incluidos previamente en el modelo.

No todas las variables aleatorias empleadas en la definción de un modelo son de interés para el analista y a veces puede ser muy pesado almacenarlas físicamente en el disco, por lo que no hay necesidad de hacerlo, pues en una cadena de Markov sólo es necesario conocer el último valor generado. Por este motivo el método con el que se añade una variable aleatoria incluye otro argumento que indique si se quiere o no almcenarla en la MCMC.

  //Adds a random variable to the model. If argument <storedInMcmc> is true it will be stored at Markov
  //chain matrix into a disk binary file.
  Real model::AddRandVar(@RandVar a, Real storedInMcmc);

El método para añadir una relación será el siguiente

  //Adds a conditioning relation
  Real model::AddRelation(@Relation r);

Casos particulares y ejemplos

A continuación se describen conceptualmente los elementos utilizados habitualmente en modelos de regresión bayesiana, clasificados funcionalmente según la metodología a emplear en cada uno.

La varianza de una regresión lineal normal

El bloque de varianzas, con distribución chi-cuadrado inversa condiciona al bloque normal modificando directamente el valor de la varianza mientras que el bloque lineal condiciona al de varianzas modificando el parámetro de escala poniendo el valor de la suma de cuadrados de los residuos homocedásticos. Este sería un caso que podríamos llamar condicionamiento simétrico pues cada uno condiciona al otro y suele aparecer cuando se aplica un ​prior conjugado.

Datos omitidos en una regresión lineal

Cuando hay omitidos la regresión es en realidad bilineal y es complicado simular conjuntamente pero es muy sencillo hacerlo condicionalmente en dos bloques, el principal (anfitrión) y el de omitidos (parásito).

Obsérvese que el bloque anfitrión no tendría porqué ser una regresión, sino que podría ser cualquier tipo de bloque que contenga una matriz de datos. El bloque de omitidos sólo tiene que tener la referencia del bloque principal, un identificador del miembro a modificar, y una lista con ubicación de los omitidos dentro del mismo.

Este esquema es ampliable al caso en el que varios bloques compartan uno o más omitidos, siempre y cuando se trate de bloques independientes entre sí. Simplemente habría que sumar las log-verosimilitudes de cada uno de ellos. Esta situación sucede con naturalidad en modelos jerárquicos en los que distintos nodos comparten un input y en modelos encadenados en los que el output de un nodo es input de otro.

Efectos aditivos en términos originales

Es muy habitual que haya que aplicar cierta transformación instantánea al output de una regresión lineal para conseguir residuos homocedásticos. Pero luego puede ocurrir que existan efectos que ocurren en términos originales y otros en términos transformados

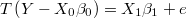
Lo único que tiene que hacer el filtro parásito es modificar el output completo del bloque anfitrión.

Ecuación en diferencias

En modelos de series temporales, tanto en el caso de la función de transferencia con deltas como el caso ARIMA hay que resolver una ecuación en diferencias

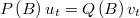
por lo que sería lógico plantear un bloque genérico que diera servicio a ambos casos.

Los parámetros de este bloque se clasifican en:

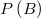• : coeficientes del numerador
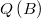• : coeficientes del denominador
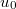• : valores iniciales del numerador
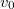• : valores iniciales del denominador

Hay que tener en cuenta que ambos polinomios podrían venir factorizados en varias estacionalidades, pero al fin y al cabo todo se reduce a coeficientes y a una estructura que rellenar con ellos y que contendría también las diferencias si las hubiere.

El denominador ha de ser siempre estacionario, pero el numerador de una función de transferencia puede ser completamente arbitrario mientras que el de un ARIMA debe ser estacionario siempre.

En el caso ARIMA caso el bloque de regresión sería el bloque parasitario y tendría que modificar la serie de ruido ARIMA (denominador) tomada de la regresión para construir los residuos (denominador). El bloque ARIMA sería a su vez parasitario de un bloque de resiudos normales.

En cambio, en el caso de función de transferencia, el bloque parasitario sería el de la ecuación en diferencias que tendría que modificar una columna de la matriz de inputs del bloque de regresión utilizando la serie del denominador, mientras que el numerador sería el input original.

Relaciones jerárquicas lineales

Sea una relación jerárquica lineal extendida

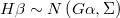
en la que 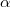son las variables latentes del nivel superior y 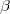las de nivel inferior definidas en uno o varios bloques, y que pueden ser a su vez latentes o primarias.

El bloque de nivel inferior condiciona a todos sus superiores modificando valor actual de las 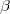. De esta forma nos quedaría en el superior una regresión lineal en la que el output sería 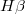, es decir, que iría cambiando en cada iteración.

La función de log-verosimilitud del nivel inferior debe llamar aditivamente a todas las de los de nivel superior en las que interviene y sumarse a su propia log-verosimilitud.

Información a priori

En el caso de haber información a priori sobre los parámetros de un bloque cualquiera habría que sumar la log-verosimilitud correspondiente a su distribución. Lo ideal es usar un ​prior conjugado siempre que sea posible.

Habría que estudiar la posibilidad de utilizar esta información en la generación de candidatos para evitar atascos en la cadena de Markov.

Prior normal

Es el más habitual de los prior pues es aplicable en muchos ambientes pues la distribución normal es autoconjugada y el grueso de los parámetros de un modelo suele ser normal. Cuando no se conoce la forma analítica de la distribución o es complicado deducir el prior conjugado, pero se puede considerar razonable que ha de ser simétrica, entonces el prior normal es sin duda la mejor opción.

Prior inverse scaled chi-square

Esta es la opción para indicar el conocimiento adquirido sobre la varianza de una distribución normal.

Restricciones deterministas

Las restricciones deterministas se implementan como una uniforme en la región factible. Para evitar problemas numéricos se utiliza el ​método de las penalizaciones de forma análoga a su empleo en las técnicas de optimización.

La log-verosimilitud en la región factible es cero pero fuera de ella en lugar de ser 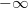será un número negativo proporcional a la distancia a la frontera, que irá creciendo durante la etapa inicial de burning hasta alcanzar un valor de penalización suficientemente grande como para que a partir de ese momento resulte altamente improbable que se genere una muestra no factible.

No debe usarse una restricción determinista si no hay un motivo que lo justifique plenamente. Por ejemplo, si un coeficiente del modelo es una probabilidad está claro que debe estar entre 0 y 1, si es una temperatura en grados kelvin o unaa velocidad entonces debe ser mayor o igual que 0, etc. Si lo que se quiere expresar es algo subjetivo o impreciso, como que que es muy improbable que una variable este fuera de un rango, entonces se debe utilizar un prior aleatorio, como una normal con una media y una desviación que se adapte a esa intuición.

////////////////////////////////////////////////////////////////////////////////
Class @Constraint : @RandomVar
////////////////////////////////////////////////////////////////////////////////
{
  Static Real _.penalty.initial = 1;
  Static Real _.penalty.factor = 1.1;
  Real _.penalty = ?;

  //////////////////////////////////////////////////////////////////////////////
  Real _penalty_update(Real numSim)
  //////////////////////////////////////////////////////////////////////////////
  {
    Real _.penalty := If(numSim==1, 
      _.penalty.initial, 
      _.penalty.factor * _.penalty) 
  };

  //////////////////////////////////////////////////////////////////////////////
  Real _penalty_eval(VMatrix g)
  //////////////////////////////////////////////////////////////////////////////
  {
    VMatrix out = GE(g,0);
    Real G.out = VMatSum(g$*out);
    If(G.out<=0, 0, -_.penalty*G.out) 
  }

  Real _penalty_log_likelihood(VMatrix g)
};

////////////////////////////////////////////////////////////////////////////////
Class @Eq : @Constraint
////////////////////////////////////////////////////////////////////////////////
{
  //////////////////////////////////////////////////////////////////////////////
  // Returns 0 if g==0 and a huge negative value in other case
  Real _penalty_log_likelihood(VMatrix g)
  //////////////////////////////////////////////////////////////////////////////
  {
    _penalty_eval(g^2)
  }
};

////////////////////////////////////////////////////////////////////////////////
// Restricciones deterministas de punto fijo
// x = cte
Class @Eq.Fixed : @Eq
////////////////////////////////////////////////////////////////////////////////
{
  VMatrix _.point;
  Real _log_likelihood(VMatrix x)
  {
    _penalty_log_likelihood(x-_.point) 
  }
};

////////////////////////////////////////////////////////////////////////////////
// Restricciones deterministas de punto fijo
// A*x = a
Class @Eq.Linear : @Eq
////////////////////////////////////////////////////////////////////////////////
{
  VMatrix _.A;
  VMatrix _.a;         
  Real _log_likelihood(VMatrix x)
  {
    _penalty_log_likelihood(_.A*x-_.a) 
  }
};

////////////////////////////////////////////////////////////////////////////////
Class @Ineq : @Constraint
////////////////////////////////////////////////////////////////////////////////
{
  //////////////////////////////////////////////////////////////////////////////
  // Returns 0 if g<=0 and a huge negative value in other case
  Real _penalty_log_likelihood(VMatrix g)
  //////////////////////////////////////////////////////////////////////////////
  {
    _penalty_eval(g)
  }
};

////////////////////////////////////////////////////////////////////////////////
// Restricciones deterministas de dominio (intervalo o rango)
// _.lower <= x <= _.upper
Class @Ineq.Domain : @Ineq
////////////////////////////////////////////////////////////////////////////////
{
  VMatrix _.lower;
  VMatrix _.upper;         
  Real _log_likelihood(VMatrix x)
  {
    VMatrix g1 = x - _.upper;
    VMatrix g2 = _.lower - x;
    _penalty_log_likelihood(g1<<g2) 
  }
};

////////////////////////////////////////////////////////////////////////////////
// Restricciones deterministas de desigualdad lineal 
// _.A x <= _.a
Class @Ineq.Linear : @Ineq
////////////////////////////////////////////////////////////////////////////////
{
  VMatrix _.A;
  VMatrix _.a;         
  Real _log_likelihood(VMatrix x)
  {
    _penalty_log_likelihood(_.A*x-_.a) 
  }
};

Modelo de regresión normal con prior conjugado para la varianza

////////////////////////////////////////////////////////////////////////////////
// Modelo de regresión normal con prior conjugado para la varianza
@Model Create.LinReg.Normal(
  VMatrix Y, //Output
  VMatrix X  //Input     )
////////////////////////////////////////////////////////////////////////////////
{
  @Model model = @Model::New(?);
  MWG::@Model model = MWG::@Model::New(?);

  Real m = VRows(Y);
  Real n = VColumns(X);
  
  MWG::@PRI.InvScaChiSquare sigma2 = [[
    VMatrix _.drawn = Mat2VMat(Col(sigma2.0));
    Real _.freeDeg = m;
    Real _.scale = sigma2.0 ]];

  MWG::@PRI.Normal residuals = [[
    VMatrix _.drawn = residuals.0;
    Real _.nu = 0;
    Real _.sigma = Sqrt(sigma2.0) ]];
  
  MWG::@RVOV.LinReg beta = [[
    VMatrix _.drawn = beta.0;
    Set _.Y = [[Y]];
    Set _.X = [[X]];
    Set _.e = [[residuals]] ]];

  Real model::addRandVar(beta,   True);
  Real model::addRandVar(sigma2, True);

  Real { model::addRelation(MWG::@Relation.Assign rel = [[
    Text _.type = "Real";
    Text _.from = "sigma2";
    Text _.to = "beta";
    Text _.expr = "((beta::_.e)[1])::_.sigma := Sqrt(VMatDat(sigma2::_.drawn,1,1))" ]]) };

  Real { model::addRelation(MWG::@Relation.Assign rel = [[
    Text _.type = "Real";
    Text _.from = "beta";
    Text _.to = "sigma2";
    Text _.expr = "sigma2::_.scale := VMatSum((beta::filter(beta::_.drawn))^2)" ]]) };
  model
};