Estrategias de estimación

Las estrategias de estimación de modelos estadísticos que manejamos en TOL, o podemos manejar en un futuro próximo, son a grandes rasgos las siguientes:

• Optimización: Todos los métodos son en realidad aproximaciones, normalmente iterativas, pues los métodos exactos (simbólicos) sólo sirven para casos de juguete. Clasificaremos estos métodos según varios criterios
  • Por el tipo de restricciones que admite el método:
    • FO (Free Optimization): No se admite ningún tipo de restricciones. Son los algoritmos más básicos como el de Newton o el de Marquardt.
    • BO (Bounded Optimization): Sólo se admiten restricciones de dominio .
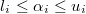    • LICO (Linear Inequality Constrained Optimization): Se admiten restricciones de desigualdad lineal.
    • AICO (Arbitrary Inequality Constrained Optimization): Se admiten restricciones de desigualdad lineal y no lineal.
    • LECO (Linear Equality Constrained Optimization): Se admiten restricciones de igualdad lineal.
    • AECO (Arbitrary Equality Constrained Optimization): Se admiten restricciones de igualdad lineal y no lineal.
  • Clasificación por la función objetivo a optimizar: Para un mismo modelo se pueden construir muchas funciones de medición de su calidad. La medida más adecuada desde el punto de vista estadístico es la verosimilitud, aunque hay quienes prefieren optimizar directamente la función de decisión para la que se desea construir el modelo. Aquí nos restringiremos a la verosimilitud, pero no siempre es sencillo ni eficiente calcular esa función:
    • AML (Aproximated Maximum Likelihood): Optimización, normalmente por mínimos cuadrados, de una función que aproxima la verosimilitud, sin que exista una forma sistemática de cuantificar el error de la aproximación. Es el caso de Estimate y de la mayoría de estimadores de modelos no lineales más o menos complejos, que se dicen máximo-verosímiles pero que en realidad optimizan algo que se intenta parecer lo más posible a la verosimilitud, muchas veces con poco éxito. Estimate se aproxima bastante bien en la mayoría de los casos, tanto que no es descabellado encasillarlo en el siguiente apartado.
    • MLE (Maximum Likelihood Estimation): Optimización de la función de verosimilitud exacta. A veces se le llama EML (Exact Maximum Likelihood) para especificar que es un MLE de verdad y no un AML disfrazado de MLE. Es el caso de los métodos de regresión lineal pura y de las funciones Logit y Probit de TOL.
  • Clasificación por el ámbito del óptimo buscado:
    • Local: Nos conformamos con un óptimo local o bien sabemos que la función objetivo es unimodal. La mayoría de los métodos son de esta categoría. De hecho, muchos de ellos, como Newton, necesitan que la función sea unimodal para garantizar la convergencia.
    • Global: Necesitamos el máximo global, o al menos el máximo en un hiperrectángulo, y no podemos asegurar que la función objetivo es unimodal. Sólo el paquete NonLinGloOpt es capaz de aportar a TOL métodos de este tipo.
  • Clasificación por el grado de derivación mínimo necesario para ejecutar las iteraciones, y por lo tanto la clase analítica mínima de la función objetivo:
    • GF (Gradient Free): No necesitan conocer el gradiente ni exacto ni aproximado. Basta con que la función objetivo sea continua, o sea de clase C0.
    • GB (Gradient Based): Precisan conocer el gradiente analítico de la función para ser eficientes, aunque normalmente funcionan bien aproximándolo. La función objetivo debe ser de clase C1 al menos.
    • HB (Hessian Based): Precisan conocer el gradiente analítico de la función para ser eficientes, aunque algunos pocos funcionan bien aproximándolo. La función objetivo debe ser de clase C2 al menos. El paquete TolIpopt dará proximamente cobertura a estos métodos.
  • Clasificación por el alcance de las iteraciones
    • MB (Mono Block): En cada iteración se tienen en cuenta todas las variables.
    • BI (Block Iterative): En cada iteración se optimiza parcialmente un bloque de variables condicionados al resto. Puede ser muy útil
      • cuando resulta complicado implementar la función conjunta, o bien
      • es más difícil de optimizar el todo que las partes, o bien
      • si se quiere paralelizar los cálculos.
• Simulación bayesiana:
  • Tipo Montecarlo: Las muestras generadas deben ser ponderadas para ser usadas en la inferencia.
  • Tipo MCMC (Markov Chain MonteCarlo): Las cadenas generadas se pueden usar directamente como una muestra de la distribución objetivo.
    • Metropolis y derivados: Sólo es necesario conocer el logaritmo de la verosimilitud conjunta salvo una constante. Es el caso de GrzLinModel y QltvRespModel.
    • Gibbs: Se dividen las variables en bloques de tal forma que somos capaces de simular cada uno en función del resto. Es el caso del BSR original.
    • Metroplis within Gibbs: El modelo se divide en bloques de variables como en Gibbs pero dentro de cada uno se simula mediante un método tipo Metropolis, en el que se utiliza la log-verosimilitud salvo constante de la distribución condicionada al resto de bloques. BSR admite este método pero sólo para los bloques lineales por el momento (bloque principal y omitidos).