Opened 14 years ago
Closed 13 years ago
#1246 closed doubt (fixed)
Estimación un modelo Logit con BSR
| Reported by: | imendez | Owned by: | Víctor de Buen Remiro |
|---|---|---|---|
| Priority: | high | Milestone: | Mantainance |
| Component: | BSR | Version: | 2.0.1 |
| Severity: | major | Keywords: | |
| Cc: | jsperez, Pedro Gea, atorre@… |
Description (last modified by )
Hola, ¿se puede estimar un modelo Logit con BSR?
Creo que los modelos Logit se pueden estimar con funciones como Logit (por máxima verosimilitud) y con el paquete GrzLinModel (de forma bayesiana y por máxima verosimilitud), pero tengo entendido que esas alternativas no permiten, por ejemplo, la introducción de jerarquías, ¿verdad?.
Si no se puede estimar actualmente un modelo Logit con BSR y es posible mejorar BSR para estimar este tipo de modelos, aprovecho este ticket para solicitar su implementación.
Un saludo.
Change History (13)
comment:1 Changed 14 years ago by
| Description: | modified (diff) |
|---|
comment:2 Changed 14 years ago by
Me temo que es del todo imposible retorcer un Logit para ser estimado con BSR.
La única forma de hacer lo que quieres sería introducir las jerarquías en GrzLinModel.
Voy a estudiar la viabilidad de este enfoque.
comment:3 Changed 14 years ago by
| Cc: | jsperez Pedro Gea added |
|---|---|
| Status: | new → accepted |
GrzLinModel está diseñado para funcionar como un sólo bloque de variables, el único que aparece en un modelo lineal generalizado, que es el del filtro lineal. Para introducir las jerarquías de una forma similar a lo que hace BSR habría que montar algo tan complejo o más como el propio BSR, pues habría de manejar distribuciones no normales. La complicación está pues en añadir nuevos bloques de variables.
Por eso GrzLinModel admite restricciones y prior sin problemas, pero no jerarquías ni omitidos, ni bloque de varianzas, ni ARIMA, ni filtros no lineales ni nada por el estilo. Esto es algo que habrá que hacer en su día pero será más bien otro sistema que tome a GrzLinModel como simulador de un bloque concreto y se ocupe luego del resto de cosas.
Sin embargo, a nivel interno resultaría relativamente sencillo añadir un tipo de prior normal vectorial sobre una combinación lineal cualquiera de las variables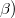 
del modelo lineal generalizado.
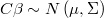
Esto permitiría introducir algunos tipos de relaciones jerárquicas muy sencillas como las típicas en las que se quiere forzar que ciertas variables se parezcan entre sí. Normalmente se suelen expresar añadiendo una variable latente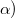 
y un segmento de regresión normal para expresar la restricción estocástica:
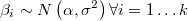
tal como sucede por ejemplo en BSR.
Sin embargo, dichas ecuaciones se pueden expresar de un modo alternativo que no precisa de ninguna variable latente, y es por tanto un prior puro, aunque vectorial en lugar de los típicos escalares que se suelen plantear
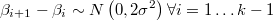
Este prior normal es expresable como un prior normal vectorial como el expresado antes tomando:
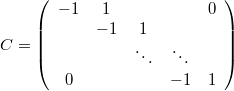
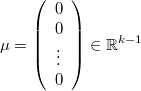
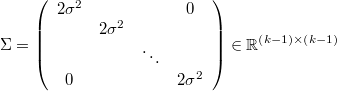
La varianza del nodo latente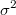 
no podría ya ser una variable sino que tendría que ser fija, y la media 
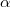no aparece por ningún lado aunque podría calcularse posteriormente como la media de los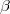 
Para otros tipos de relaciones jerárquicas o reticulares podría estudiarse si existe un diseño alternativo de este tipo.
comment:4 Changed 14 years ago by
Habría que determinar varias cosas antes de afrontar este problema:
- ¿Se sabe que el modelo ha de ser Logit y no Probit o no se ha estudiado? Si sirve el probit se puede hacer con BSR sin problemas aunque GrzLinModel es mucho más rápido pues ataca el problema directamente sin subterfugios, ya que está diseñado precisamente para esa clase de modelos.
- ¿Sería suficiente con el tipo de relaciones jerárquicas planteadas anteriormente?
- ¿Cómo de urgente e importante sería implementarlo?
comment:5 Changed 14 years ago by
| Cc: | atorre@… added |
|---|
comment:6 Changed 14 years ago by
Aunque la idea de eliminar la variable latente es correcta, hay un pequeño problema en la forma de eliminarla y en el diseño alternativo que se desprende de ello. Cada variable queda ligada a la anterior por lo que la distancia entre variables podría ir creciendo entre las más alejadas. Además de eso la matriz de covarianzas no podría ser diagonal sino tridiagonal, puesto que cada componente está relacionada con la siguiente.
Para evitarlo habría que sustituir las ecuaciones por otras más simétricas, que establecieran que cada variable se mantenga alrededor de la media del resto de variables.
He reescrito las ecuaciones en la página wiki del paquete BysPrior donde voy a programar la solución de este problema para que sea aplicable también en otros simuladores que puedan surgir fuera de GrzLinModel.
comment:11 Changed 14 years ago by
comment:13 Changed 13 years ago by
| Resolution: | → fixed |
|---|---|
| Status: | accepted → closed |
No es posible estimar un Logit con BSR porque BSR sólo admite la distribución normal para los residuos. En el caso Probit, mediante un filtro no lineal, es posible
transformar la regresión booleana en una regresión lineal normal, tal y como se explica en el apartado 6.3.4 de la página 51 del manual de BSR.
Pero eso no es posible con un Logit, o al menos a mí no se me ha ocurrido cómo. Quizás podría pesarse en alguna forma de aproximación mediante algún tipo de transformación. Lo pensaré.