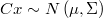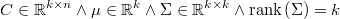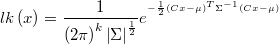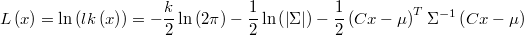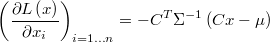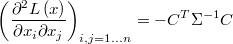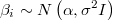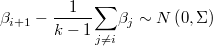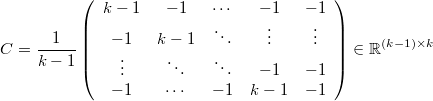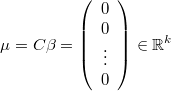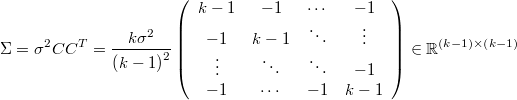close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

  1. Package BysPrior
    1. Deterministic priors
      1. Domain prior
      2. Polytope prior
      3. Non linear constraining prior
    2. Random priors
      1. Multinormal prior
        1. Hierarquical relation of simple homogenity
      2. Transformed prior
    3. Composed priors

Package BysPrior

BysPriorInf stands for Bayesian Prior Information and allows to define prior information handlers to be used in estimation systems (max-likelihood and bayesian ones).

A prior is a distribution function over a subset of the total set of variables of a model that expresses the knowledge about the phenomena behind the model.

The effect of a prior is to add the logarithm of its likelihood to the logarithm of the likelihood of the global model. So it can be two or more priors over some variables. For example, in order to stablish a truncated normal we can define a uniform over the feasible region and an unconstrainined normal.

In order to be estimated with NonLinGloOpt (max-likelihood) and BysSampler (Bayesian sampler), each prior must define methods to calculate the logarithm of the likelihood (except an additive constant), its gradient and its hessian, and an optional set of constraining inequations, in order to define the feasible region. Each inequation can be linear or not, but then the gradient must be also calculated. Note that this implies that priors should be continuous and two times differentiable and restrictions must be continuous and differerentiable, but this is an admisible restricion in almost all cases.

In the base class will be the tools to index the subset of variables affected by prior in the vector of all model variables. Thus prior methods can be programmed as if there were only them, driving a simple vector.

Deterministic priors

Very often it is possible to know that a variable should be in a certain range or belonging to a particular region of space. This kind of deterministic knowledge can be expressed as a constrained uniform distribution.

Let x a uniform random variable in a region \Omega\in\mathbb{R}^{n} which likelihood function is

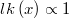
lk\left(x\right) \propto 1

Since the logarithm of the likelihood but a constant is zero, when log-likelihood is not defined for a prior, the default assumed will be the uniform distribution, also called non informative prior.

Domain prior

The easiest way, but one of the most important, to define a non informative prior, is to stablish a domain interval for one or more variables.

bounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image000.png 		unbounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image001.png

In this cases, you mustn't to define the log-likelihood nor the constraining inequation functions, but simply it's needed to fix the lower and upper bounds:

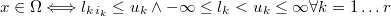
x\in\Omega\Longleftrightarrow l_{k}\leqx_{i_k}\leq u_{k}\wedge-\infty\leq l_{k}<u_{k}\leq\infty\forall k=1\ldots r

If both lower and upper bounds are non finite, then we call it the neutral prior, that is equivalent to don't define any prior.

If all lower and upper bounds are finite, then the fesasible region is an hyperrectangle.

Polytope prior

A polytope prior is defined by a system of compatible linear inequalities

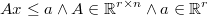
Ax\leq a\wedge A\in\mathbb{R}^{r\times n}\wedge a\in\mathbb{R}^{r}

bounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image003.png 		unbounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image002.png

An special and common case of polytope region is the defined by order relations like

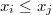
x_{i}} \leq x_{j}}

We can implement this type of prior by means of a set of r inequations but, since NonLinGloOpt doesn't have any special behaviour for linear inequations, it could be an inefficient implementation. However we can define just one non linear inequation that is equivalent to the full set of linear inequations.

If we define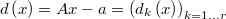

d\left(x\right)=Ax-a=\left(d_{k}\left(x\right)\right)_{k=1\ldots r} then

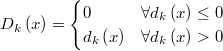D_{k}\left(x\right)=\begin{cases} 0 & \forall d_{k}\left(x\right)\leq0\\ d_{k}\left(x\right) & \forall d_{k}\left(x\right)>0\end{cases}

is a continuous function in 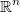\mathbb{R}^{n} and

D_{k}^{3}\left(x\right)=\begin{cases} 0 & \forall d_{k}\left(x\right)\leq0\\ d_{k}^{3}\left(x\right) & \forall d_{k}\left(x\right)>0\end{cases}

is continuous and differentiable in 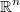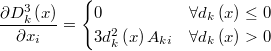\mathbb{R}^{n}

\frac{\partial D_{k}^{3}\left(x\right)}{\partial x_{i}}=\begin{cases} 0 & \forall d_{k}\left(x\right)\leq0\\ 3d_{k}^{2}\left(x\right)A_{ki} & \forall d_{k}\left(x\right)>0\end{cases} 		source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image004.png

The feasibility condition can be defined as a single nonlinear inequality continuous and differentiable everywhere

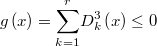
g\left(x\right)=\underset{k=1}{\overset{r}{\sum}}D_{k}^{3}\left(x\right)\leq0

The gradient of this function is

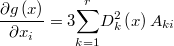
\frac{\partial g\left(x\right)}{\partial x_{i}}=3\underset{k=1}{\overset{r}{\sum}}D_{k}^{2}\left(x\right)A_{ki}

Non linear constraining prior

We can express any set of arbitrary non linear constraining inequations defining as

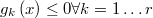
g_{k}\left(x\right)} \leq 0 \forall k=1 \dots r

In this case we need to define also the gradient of each one.

bounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image005.png 		unbounded region
source:/tolp/OfficialTolArchiveNetwork/BysPrior/doc/image006.png

Random priors

When you have a vague idea of where it could be a variable, it is possible to express by a probability distribution consistent with that knowledge.

Multinormal prior

When we know that a single variable should fall symmetrically close to a known value we can express telling that it have a normal distribution with average in these value. This type of prior knowledge can be extended to higher dimensions by the multinormal distribution over a linear combination of variables

C x\sim N\left(\mu,\Sigma\right) C\in\mathbb{R}^{k\times n}\wedge\mu\in\mathbb{R}^{k}\wedge\Sigma\in\mathbb{R}^{k\times k}\wedge\mathrm{rank}\left(\Sigma\right)=k

which likelihood function is

lk\left(x\right)=\frac{1}{\left(2\pi\right)^{k}\left|\Sigma\right|^{\frac{1}{2}}}e^{^{-\frac{1}{2}\left(Cx-\mu\right)^{T}\Sigma^{-1}\left(Cx-\mu\right)}}

The log-likelihood is

L\left(x\right)=\ln\left(lk\left(x\right)\right)=-\frac{k}{2}\ln\left(2\pi\right)-\frac{1}{2}\ln\left(\left|\Sigma\right|\right)-\frac{1}{2}\left(Cx-\mu\right)^{T}\Sigma^{-1}\left(Cx-\mu\right)

The gradient is

\left(\frac{\partial L\left(x\right)}{\partial x_{i}}\right)_{i=1\ldots n}=-C^{T}\Sigma^{-1}\left(Cx-\mu\right)

and the hessian

\left(\frac{\partial^{2}L\left(x\right)}{\partial x_{i}\partial x_{j}}\right)_{i,j=1\ldots n}=-C^{T}\Sigma^{-1}C

Hierarquical relation of simple homogenity

If we want to express that a certain group of variables 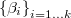\left\{ \beta_{i}\right\} _{i=1\ldots k} are independent and normally distributed with unknow average and fixed standard deviation the usual way is to define a new latent variable 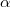\alpha representing the average

\beta_{i}\sim N\left(\alpha,\sigma^{2}I\right)

If there is not posible to use a hierarquical simulation engine we can rewrite these relations removing the latent variable and setting that each variable must be around the average of the rest of them with certain covariance matrix

\beta_{i+1}-\frac{1}{k-1}\underset{j\neq i}{\sum}\beta_{j}\sim N\left(0,\Sigma\right)

Then it's posible to write this as an special case of multinormal prior over a linear combination of variables taking

C=\frac{1}{k-1}\left(\begin{array}{ccccc}k-1 & -1 & \cdots & -1 & -1\\-1 & k-1 & \ddots & \vdots & \vdots\\\vdots & \ddots & \ddots & -1 & -1\\-1 & \cdots & -1 & k-1 & -1\end{array}\right)\in\mathbb{R}^{\left(k-1\right)\times k}

\mu=C\beta=\left(\begin{array}{c}0\\0\\\vdots\\0\end{array}\right)\in\mathbb{R}^{k}

\Sigma=\sigma^{2}CC^{T}=\frac{k\sigma^{2}}{\left(k-1\right)^{2}}\left(\begin{array}{cccc}k-1 & -1 & \cdots & -1\\-1 & k-1 & \ddots & \vdots\\\vdots & \ddots & \ddots & -1\\-1 & \cdots & -1 & k-1\end{array}\right)\in\mathbb{R}^{\left(k-1\right)\times\left(k-1\right)}

Transformed prior

Sometimes we have an information prior that has a simple distribution over a transformation of original variables. For example, if we know that a set of variables has a normal distribution with average equal to another variable, as in the case of latent variables in hierarquical models

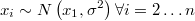
x_{i}\sim N\left(x_{1},\sigma^2\right)\forall i=2\ldots n

Then we can define a variable transformation like this

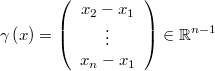
\gamma \left(x\right)=\left(\begin{array}{c} x_{2}-x_{1}\\ \vdots\\ x_{n}-x_{1}\end{array}\right)\in\mathbb{R}^{n-1}

and define the simple normal prior

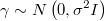
\gamma\sim N\left(0,\sigma^{2}I\right)

Then the log-likelihood of original prior will be calculated from the transformed one as

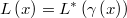
L\left(x\right)=L^{*}\left(\gamma\left(x\right)\right)

If we know the first and second derivatives of the transformation

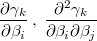
\frac{\partial\gamma_{k}}{\partial\beta_{i}}\, , \;\frac{\partial^{2}\gamma_{k}}{\partial\beta_{i}\partial\beta_{j}}

then we can calculate the original gradient and the hessian after the gradient and the hessian of the transformed prior as following

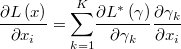
\frac{\partial L\left(x\right)}{\partial x_{i}}=\underset{k=1}{\overset{K}{\sum}}\frac{\partial L^{*}\left(\gamma\right)}{\partial\gamma_{k}}\frac{\partial\gamma_{k}}{\partial x_{i}}

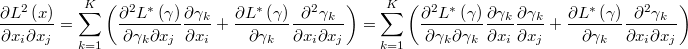
\frac{\partial L^{2}\left(x\right)}{\partial x_{i}\partial x_{j}}=\underset{k=1}{\overset{K}{\sum}}\left(\frac{\partial^{2}L^{*}\left(\gamma\right)}{\partial\gamma_{k}\partial x_{j}}\frac{\partial\gamma_{k}}{\partial x_{i}}+\frac{\partial L^{*}\left(\gamma\right)}{\partial\gamma_{k}}\frac{\partial^{2}\gamma_{k}}{\partial x_{i}\partial x_{j}}\right)=\underset{k=1}{\overset{K}{\sum}}\left(\frac{\partial^{2}L^{*}\left(\gamma\right)}{\partial\gamma_{k}\partial\gamma_{k}}\frac{\partial\gamma_{k}}{\partial x_{i}}\frac{\partial\gamma_{k}}{\partial x_{j}}+\frac{\partial L^{*}\left(\gamma\right)}{\partial\gamma_{k}}\frac{\partial^{2}\gamma_{k}}{\partial x_{i}\partial x_{j}}\right)

Thus it is possible to define a variety of information a priori from a pre-existing instance of a transformation defined with their first and second derivatives.

For example we can define a log-normal prior without to define explicitly its log-likelihood, gradient and hessian.

Composed priors

If you have a set of priors you can express as just one by means of

  • merge the subsets of used variables
  • add the log-likelihood functions, the gradients and the hessians,
  • concat the set of constraining inequations
  • take the maximum of lower bounds
  • take the minimum of upper bounds

Last modified 14 years ago Last modified on Jun 16, 2011, 3:31:41 PM