close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

  1. Package BysSampler
    1. Introducción
    2. Jerarquía de clases con base en Class @Generic
      1. Class @AcceptReject
        1. Class @RandWalk
        2. Class @RandWalk.InPolytope
        3. Class @RandRay
        4. Class @GriddyGibbs
      2. Class @MetHas
        1. Class @MetHas.RandWalk
      3. Class @MulTryMet
        1. Class @MulTryMet.Symmetric
          1. Class @MulTryMet.RandWalk
          2. Class @MulTryMet.RandRay
      4. Class @GenMulTryMet
        1. Class @GenMulTryMet.Symmetric
          1. Class @GenMulTryMet.RandRay
      5. Class @Arima
        1. @Arima.MetHas.RandWalk
        2. @Arima.MulTryMet.RandWalk
        3. @Arima.MulTryMet.RandRay

Package BysSampler

Introducción

El paquete BysSampler consiste en una jerarquía de clases para el muestreo bayesiano de cadenas de Markov de una distribución de probabilidad vectorial arbitraria, partiendo únicamente del logaritmo de la función de densidad correspondiente, a la que llamaremos densidad objetivo, y a la que se puede añadir una constante arbitraria

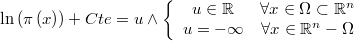
\ln\left(\pi\left(x\right)\right)+Cte=u\wedge\left\{ \begin{array}{cc}\begin{array}{c} u\in\mathbb{R}\end{array} & \forall x\in\Omega\subset\mathbb{R}^{n}\\u=-\infty & \forall x\in\mathbb{R}^{n}-\Omega\end{array}\right. $$

Existe una batería de métodos disponibles en la literatura capaces en teoría de dar respuesta a este tipo de problemas en determinadas circunstancias:

Cada uno de estos algoritmos requiere algún otro tipo de información auxiliar particular de cada caso, pero se intentará que los valores por defecto sean adecuados en la mayoría de las ocasiones, de forma que el usuario no necesite saber demasiado acerca de los detalles de cada uno, salvo en casos en los que la eficiencia o la complejidad del problema lo requieran. El objetivo final sería la implementación de un algoritmo que de forma heurística seleccionara el método más adecuado a un problema en base a sus dimensiones y a un análisis inicial de la función de densidad conjunta.

Los métodos escalares suelen ser más lentos en ejecución y además, si la región de densidad no nula es acotada, requieren la implementación de un método que proporcione los límites de cada variable condicionados a los valores actuales del resto de variables, lo cual puede ser a veces más costoso que la propia simulación.

Los métodos vectoriales en cambio sólo necesitan partir de un vector con densidad no nula. A cambio, la mayoría de ellos precisan de una distribución de probabilidad que genere candidatos plausibles que serán luego aceptados o rechazados según un criterio determinado por cada algoritmo. El sistema proporcionará un generador universal de tipo paseo aleatorio con control de tamaño de paso automático que será suficiente en la mayor parte de las ocasiones. Algunos algoritmos pueden requerir además de alguna otra función que cumpla determinadas condiciones pero para todos ellos se dará al menos una forma por defecto transparente para el usuario.

Cuando el modelo es muy complejo y está compuesto por bloques bien diferenciados lo mejor es aplicar el algoritmo más adecuado a cada uno de ellos y unir los resultados mediante el método de Gibbs.

Por último se requiere algún mecanismo de diagnosis y reparación de de la cadena generada que mejore su calidad eliminando elementos demasiado repetidos o que cribe zonas superpobladas lo cuál se explica en la página de post-procesado

Jerarquía de clases con base en Class @Generic

La clase @Generic es la clase base de la que heredan todos los simuladores.

Los métodos virtuales puros fundamentales son los que definirán el logaritmo de la función de densidad definir por el usuario para cada problema y el método de muestreo definido por el sistema para cada algoritmo 

  //Target log-density except a constant
  //This method must be redefined by end user classes in order to define
  //the specific distribution to sample
  Real pi_logDens(VMatrix z);
  //Internal drawer must be redefined by system internal classes to 
  //implement a given sampling algorithm
  VMatrix _draw(VMatrix x);

Por supuesto el usuario puede heredar sus propias clases que implementen algoritmos no suministrados por el sistema.

Opcionalmente, el usuario podrá implementar el método 

  //Will be called after each accepted or rejected simulation
  //This method can be redefined by end user classes
  Real doAfterDraw(Real void) { True };

que será llamado inmediatamente después de cada llamada al método _draw, lo cual podrá ser utilizado para tareas arbitrarias pero está especialmente indicado para montar una simulación de Gibbs por bloques, pues permite condicionar el resto de bloques al nuevo estado del bloque recién simulado

También tiene una serie de métodos virtuales puros de acceso al vector de variables de forma que se independice la metodología de simulación del mecanismo de almacenamiento de la cadena: 

  //Number of variables to be simulated
  Real get.n(Real void);
  //Returns current drawn values
  VMatrix get.x(Real void);
  //Sets current drawn values
  Real set.x(VMatrix x);

Class @AcceptReject

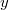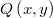La clase @AcceptReject : @Generic sirve de base a todos los métodos en los que se genera un candidato y según una función de transición a partir de la última muestra x con densidad Q\left(x,y\right) . Luego ese candidato puede ser aceptado o rechazado según cierto criterio definido por una fórmula que retorna un valor crítico de aceptación

\alpha \in \left[0,1\right]

Por último se genera una uniforme

r \sim U\left[0,1\right]

y si resulta que 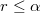r \le \alpha entonces se acepta el candidato, en cuyo caso se añadirá 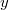y a la cadena de Markov. Si se rechaza se volverá a añadir el mismo x anterior.

Para que un método de este tipo converja efectivamente a la distribución objetivo la cadena de Markov debe ser reversible, es decir, la función de transición debe cumplir la ecuación de balance detallado (​detailed balance)

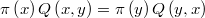
\pi\left(x\right) Q\left(x,y\right) = \pi\left(y\right) Q\left(y,x\right)

Class @RandWalk

La clase @RandWalk : @AcceptReject genera los candidatos como un paseo aleatorio en el que en cada paso se da un salto desde el último punto aceptado a otro de su entorno mediante una normal multidimensional

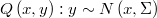Q\left(x,y\right) : y \sim N\left(x,\Sigma\right) .

Por defecto se tomará

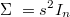
\Sigma\ = s^2 I_n

donde el tamaño de paso (step size) s será modificado en cada iteración de forma que el ratio de aceptación Real @Generic::acceptRatio, es decir, la proporción de candidatos aceptados, se acerque lo más posible a un valor óptimo o deseado Real @AcceptReject::acceptRatio.target dependiente de cada método.

Class @RandWalk.InPolytope

La clase @RandWalk.InPolytope : @AcceptReject genera los candidatos como un paseo aleatorio en el que en cada paso se da un salto desde el último punto aceptado a otro de su entorno mediante una uniforme en una hiperesfera de radio menor a la distancia mínima del punto actual hasta la fronteras de un politopo

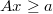
A x \ge a

Es el generador de candidatos adecuado para generar muestras sujetas a restricciones de desigualdad no lineales. En ésta página se puede ver la descripción técnica de este generador.

Class @RandRay

La clase @RandRay : @AcceptReject es similar a @RandWalk pero primero se fija un vector de dirección unitaria y luego se genera un punto en esa dirección con origen en el último valor aceptado y longitud normal de media nula

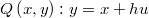
Q\left(x,y\right) : y = x + h u

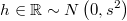
h \in \mathbb{R} \sim N\left(0,s^2\right)

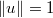
\left\Vert u \right\Vert = 1

Class @GriddyGibbs

Si en el método Random Ray en lugar de poder tomar cualquier dirección del espacio se restringe a los ejes de coordenadas en la base natural, se tiene el método de generación Griddy-Gibbs

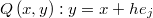
Q\left(x,y\right) : y = x + h e_j

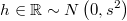
h \in \mathbb{R} \sim N\left(0,s^2\right)

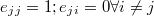
e_j_j = 1 ; e_j_i = 0 \forall i \ne j

Class @MetHas

La clase @MetHas : @AcceptReject implementa el más simple de los métodos de simulación vectorial: el método ​Metropolis-Hastings, que puede ser muy eficiente cuando no hay muchas variables y estas no están muy correlacionadas. El valor crítico de aceptación de este método se calcula como

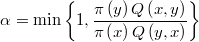
\alpha = \min \left\{ 1, \frac{ \pi\left( y \right) Q\left( x, y \right) }{ \pi\left( x \right) Q\left( y, x \right) } \right\} $$

Class @MetHas.RandWalk

Si se hereda de @RandWalk y @MetHas al mismo tiempo se obtiene la modalidad más usual: el método Random Walk Metropolis-Hastings (RWMH) cuyo valor crítico de aceptación es el cociente de densidades

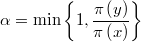
\alpha = \min \left\{ 1, \frac{ \pi\left( y \right) }{ \pi\left( x \right)} \right\} $$

Es decir, si el candidato es más probable que el punto anterior siempre es aceptado.

En este caso se tiene una fórmula que da el óptimo ratio de aceptación propuesta en el artículo ​Optimal scaling for various Metropolis-Hastings algorithms (''Gareth O. Roberts and Jeffrey S. Rosenthal'')

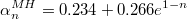
\alpha^{MH}_n = 0.234 + 0.266 e^{1-n} $$

El problema es que esta regla heurística supone realizar pruebas para diferentes valores del tamaño de paso hasta encontrar el que da el ratio de aceptación esperado, lo cual supone un coste operacional excesivo. En el ejemplo 1 se puede observar la excesiva dependencia del método con respecto al tamaño de paso.

Class @MulTryMet

La clase @MulTryMet: @AcceptReject implementa el método ​Multiple Try Metropolis (MTM) basado en generar un número 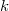k $$ de precandidatos 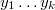y_1 \dots y_k $$ según la ley 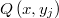Q\left(x,y_j\right) de entre los que se selecciona el candidato propiamente dicho.

En primer lugar se debe definir una función de pesos de transición

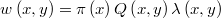
w\left( x,y \right) = \pi\left( x \right) Q\left( x,y \right)\lambda \left( x,y \right) $$

donde

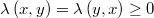
\lambda \left( x,y \right) = \lambda \left( y,x \right) \ge 0 $$

Una vez generados los precandidatos, la selección del candidato 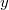y $$ se hace de forma aleatoria proporcional a los pesos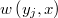 w\left( y_j, x \right) $$

Posteriormente se generan de forma recíproca los puntos 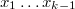x_1 \dots x_{k-1} $$ según la ley 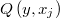Q\left(y,x_j\right) y se añade a la lista el punto de origen actual x_k = x $$.

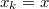Finalmente, el valor crítico de aceptación del método se calculará como

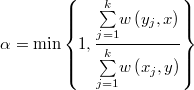
\alpha = \min \left\{ 1, \frac{ {\overset{k}{\underset{j=1}{\sum}} {w\left( y_j, x \right)}} }{{\overset{k}{\underset{j=1}{\sum}} {w\left( x_j, y \right)}} } \right\} $$

Con una buena selección del número 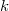k $$ de precandidatos y de la función 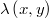\lambda \left( x,y \right) $$ se puede mejorar bastante la convergencia y disminuir la autocorrelación de la cadena con respecto al método ​Metropolis-Hastings, Evidentemente esto sucede a costa de un mayor numero de evaluaciones de la densidad por lo que no es trivial determinar el valor óptimo de k $$.

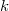Hay que hacer notar que el método MTM con 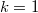k=1 $$ es precisamente el método MH, aunque por razones de eficiencia conviene tenerlos implementados por separado.

Class @MulTryMet.Symmetric

Si la función de geeración de candidatos es simétrica se puede tomar simplemente

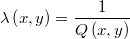
\lambda \left( x,y \right) = \frac{1}{Q\left( x,y \right)} $$

resultando que la función de pesos es la propia densidad objetivo:

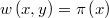
w\left( x,y \right) = \pi\left( x \right) $$

Class @MulTryMet.RandWalk

La clase @MulTryMet.RandWalk : @MulTryMet.Symmetric, @RandWalk implementa la modalidad más simple de ​Multiple Try Metropolis: el método Random Walk Multiple Try Metropolis (RWMTM).

Hasta el momento no se ha podido encontrar una fórmula del ratio de aceptación óptimo análoga a la de Roberts-Rosenthal para el método Metrópolis-Hastings, o al menos el que escribe no tiene noticias de su existencia. En el ejemplo 1 se ilustra la dependencia del método con respecto al tamaño de paso.

Class @MulTryMet.RandRay

La clase @MulTryMet.RandRay: @MulTryMet.Symmetric implementa la modalidad Random Ray Multiple Try Metropolis (RRMTM) en la que todos los precandidatos se generan en una misma dirección seleccionada aleatoriamente, de forma simular al método ​Hit and Run pero evitando la optimización unidimensional que puede resultar demasiado costosa.

Class @GenMulTryMet

La clase @GEnMulTryMet: @AcceptReject implementa el método ​Generalized Multiple Try Metropolis-Hastings (GMTM) del cual MTM es un caso particular.

La selección de precandidatos se hace igual que en MTM pero ahora los pesos se calculan con una función arbitraria con la única restricción de ser positiva.

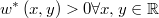
w^*\left( x,y \right) >0 \forall x,y \in \mathbb{R} $$

El candidato 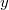y $$ se selecciona aleatoriamente con probabilidad proporcional al peso de cada precandidato

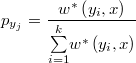
p_{y_{j}}=\frac{w^{*}\left(y_{i},x\right)} {\overset{k}{\underset{i=1}{\sum}}w^{*}\left(y_{i},x\right)} $$

Análogamente al caso MTM se generan de forma recíproca los puntos 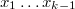x_1 \dots x_{k-1} $$ según la ley 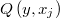Q\left(y,x_j\right) y se añade a la lista el punto de origen actual 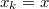x_k = x $$ y se define

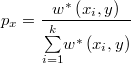
p_x =\frac{w^{*}\left(x_{i},y\right)} {\overset{k}{\underset{i=1}{\sum}}w^{*}\left(x_{i},y\right)} $$

Finalmente, el valor crítico de aceptación del método se calculará como

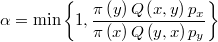
\alpha = \min \left\{ 1, \frac{ \pi\left( y \right) Q\left( x, y \right) p_x}{ \pi\left( x \right) Q\left( y, x \right) p_y} \right\} $$

La ventaja de este método es que sólo es preciso evaluar la densidad objetivo en el candidato seleccionado y no en todos los precandidatos como ocurre en el caso MTM. La eficacia del método dependerá ahora como es lógico de la función de pesos. Cuanto más parecida sea a la densidad objetivo en el entorno de x $$ mejor funcionará.

Los autores del algoritmo proponen usar una aproximación cuadrática del logaritmo de la densidad objetivo pero eso sólo tiene sentido si se dispone de una formulación analítica de esa función y aún así, si la dimensión del espacio no es muy pequeña, el uso del gradiente y el hessiano de la misma puede ser tan ineficiente o más que la propia evaluación en un gran número de precandidatos.

Class @GenMulTryMet.Symmetric

En el caso de generación simétrica de candidatos el valor crítico de aceptación del método se simplifica a

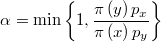
\alpha = \min \left\{ 1, \frac{ \pi\left( y \right) p_x}{ \pi\left( x \right) p_y} \right\} $$

Class @GenMulTryMet.RandRay

Si se toman los precandidatos dentro de una misma recta con dirección prefijada aleatoriamente, se puede evaluar la densidad objetivo en un pequeño subconjunto de 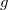g $$ puntos y usar esos valores para crear una función que aproxime la densidad en toda la recta mediante splines o con el método que se estime más oportuno.

Class @Arima

Esta clase, ideada en principio como mecanismo de chequeo del sistema, implementa los métodos necesarios para manejar un modelo en el que las variables son los coeficientes de los polinomios estacionarios de un modelo ARIMA que hay que contrastar con una serie temporal de ruido ARIMA normal. Los valores iniciales se simulan en cada paso de forma condicionada a los polinomios simulados, pues en ese caso es formulable analíticamente, pero no se almacenan como cadena de Markov. En una próxima versión podría añadirse esta capacidad de forma opcional.

@Arima.MetHas.RandWalk

Simula un modelo ARIMA con el método Random Walk Metropolis-Hastings (RWMH)

@Arima.MulTryMet.RandWalk

Simula un modelo ARIMA con el método Random Walk Multiple Try Metropolis (RWMTM)

@Arima.MulTryMet.RandRay

Simula un modelo ARIMA con el método Random Ray Multiple Try Metropolis (RRMTM)

Last modified 14 years ago Last modified on Feb 14, 2011, 5:19:56 PM