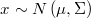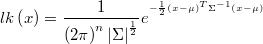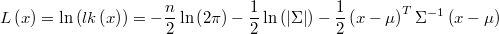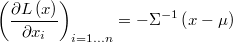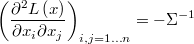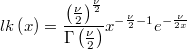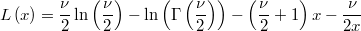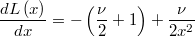| Version 12 (modified by , 15 years ago) (diff) |
|---|
Package BysPrior
BysPriorInf stands for Bayesian Prior Information and allows to define prior information handlers to be used in estimation systems (max-likelihood and bayesian ones).
A prior is a distribution function over a subset of the total set of variables of a model that expresses the knowledge about the phenomena behind the model.
The effect of a prior is to add the logarithm of its likelihood to the logarithm of the likelihood of the global model. So it can be two or more priors over some variables. For example, in order to stablish a truncated normal we can define a uniform over the feasible region and an unconstrainined normal.
In order to be estimated with NonLinGloOpt (max-likelihood) and BysSampler (Bayesian sampler), each prior must define methods to calculate the logarithm of the likelihood (except an additive constant), its gradient and its hessian, and an optional set of constraining inequations, in order to define the feasible region. Each inequation can be linear or not and the gradient must be also calculated. Note that this implies that priors should be continuous and two times differentiable and restrictions must be continuous and differerentiable, but this an admisible restricion in almost all cases.
Deterministic priors
Very often it is possible to know that a variable should be in a certain range or belonging to a particular region of space. This kind of deterministic knowledge can be expressed as a constrained uniform distribution.
Let  a uniform random variable in a region
a uniform random variable in a region
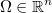 which likelihood function is
which likelihood function is
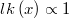
Since the logarithm of the likelihood but a constant is zero, when log-likelihood is not defined for a prior, the default assumed will be the uniform distribution, also called non informative prior.
Domain prior
The easiest way, but one of the most important, to define a non informative prior, is to stablish a domain interval for one or more variables.
bounded region | unbounded region
|
In this cases, you mustn't to define the log-likelihood nor the constraining
inequation functions, but simply it's needed to fix the lower and upper
bounds:
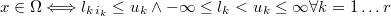
If both lower and upper bounds are non finite, then we call it the neutral prior, that is equivalent to don't define any prior.
If all lower and upper bounds are finite, then the fesasible region is an hyperrectangle.
Polytope prior
A polytope prior is defined by a system of compatible linear inequalities
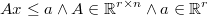
bounded region | unbounded region
|
An special and common case of polytope region is the defined by order relations like
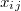
We can implement this type of prior by means of a set of  inequations but, since NonLinGloOpt
doesn't have any special behaviour for linear inequations, it could be an
inefficient implementation. However we can define just one non linear inequation
that is equivalent to the full set of linear inequations.
inequations but, since NonLinGloOpt
doesn't have any special behaviour for linear inequations, it could be an
inefficient implementation. However we can define just one non linear inequation
that is equivalent to the full set of linear inequations.
If we define 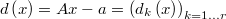 then then 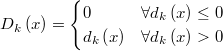 is a continuous function in 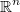 and and 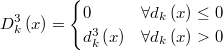 is continuous and differentiable in 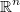 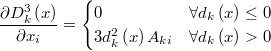 | 
|
The feasibility condition can be defined as a single nonlinear inequality continuous and differentiable everywhere
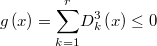
The gradient of this function is
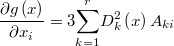
Random priors
When you have a vague idea of where it could be a variable, it is possible to express by a probability distribution consistent with that knowledge.
Multinormal prior
When we know that a single variable should fall symmetrically close to a known value we can express telling that it have a normal distribution with average in these value. This type of prior knowledge can be extended to higher dimensions by the multinormal distribution
which likelihood function is
The log-likelihood is
The gradient is
and the hessian
Inverse chi-square prior
In a model with normal waste is permissible to award the unknown variance an inverse chi-square distribution with scale parameter equal to the average of squares of residuals and freedom degrees the data length.
The likelihood is now the scalar function
The log-likelihood is
The first derivative is
The second derivative is
Transformed prior
Sometimes we have an information prior that has a simple distribution over a transformation of original variables. For example, if we know that a set of variables has a normal distribution with average equal to another variable, as in the case of latent variables in hierarquical models
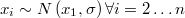
Then we can define a variable transformation like this
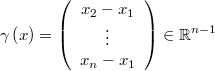
and define the simple normal prior
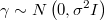
Then the log-likelihood of original prior will be calculated from the transformed one as
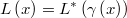
If we know the first and second derivatives of the transformation
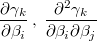
then we can calculate the original gradient and the hessian after the gradient and the hessian of the transformed prior as following
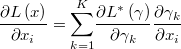
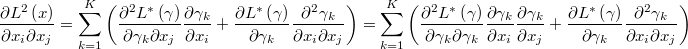
Thus it is possible to define a variety of information a priori from a pre-existing instance of a transformation defined with their first and second derivatives.
For example we can define a log-normal prior without to define explicitly its log-likelihood, gradient and hessian.