Package BysSampler

Ejemplo 01

Definición del modelo

Este ejemplo de uso de BysSampler::@MetHas.RandWalk se ha desarrollado para ilustrar la dependencia del método MH con respecto al tamaño de paso.

Se genera de forma aleatoria un modelo ARMA que podríamos calificar de bastante intrincado

AR1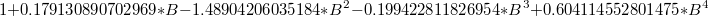
AR2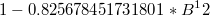
MA1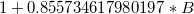
MA2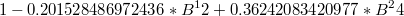

Se generan unos residuos y unos valores iniciales con los que se construye el ruido ARMA

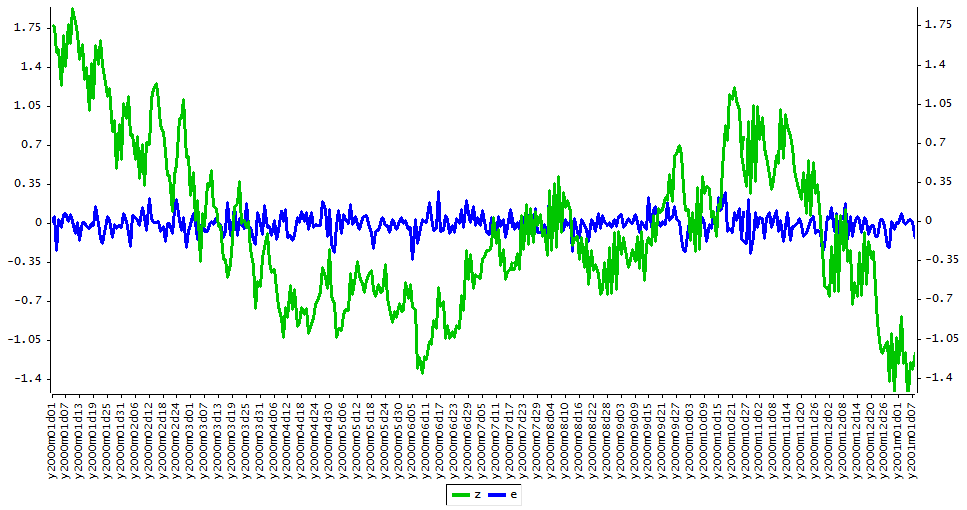
Simulación con Random Walk Metropolis-Hastings

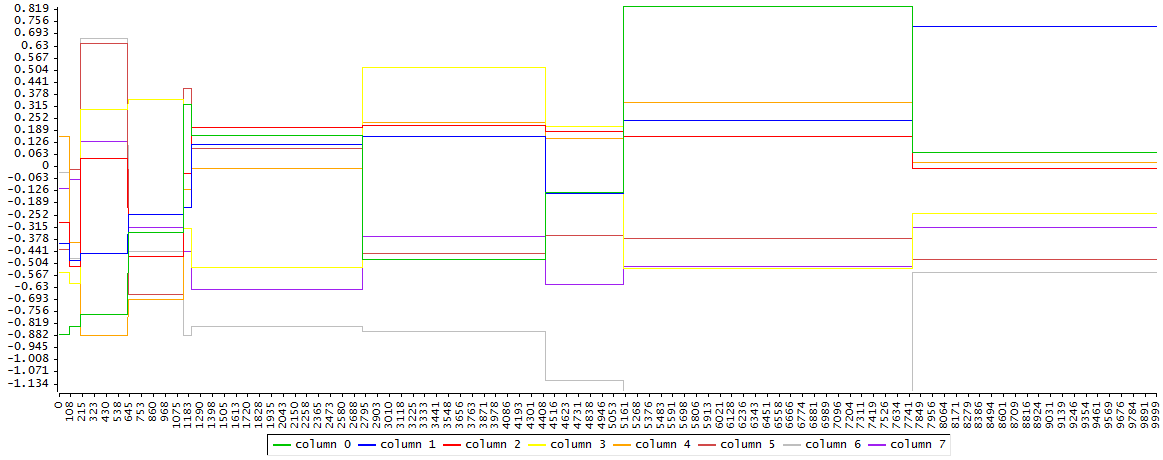
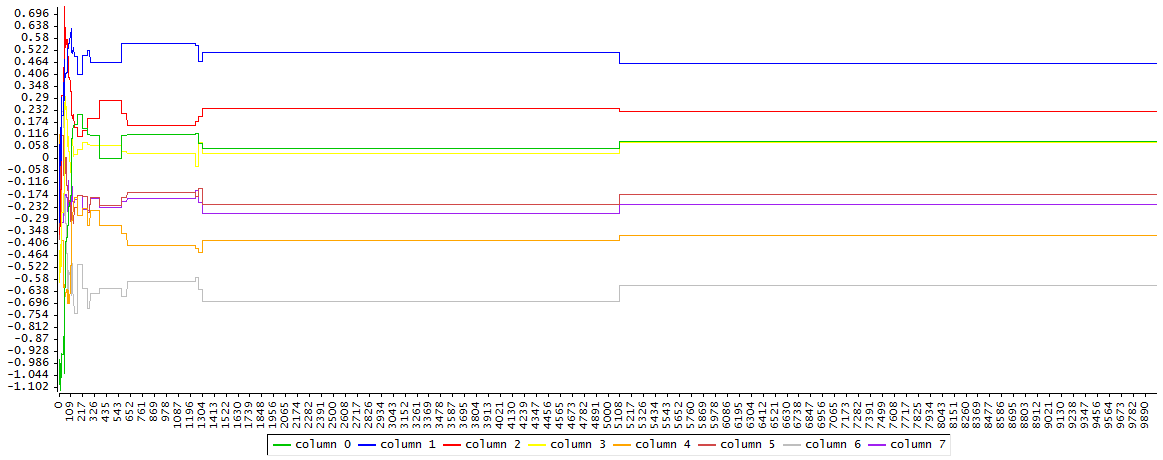
Se genera una muestra de 10000 simulaciones de los parámetros ARMA mediante el método Random Walk Metropolis-Hastings (RWMH) con tamaño de paso 1

y se observa que el nivel de aceptación es ínfimo y no hay ningún atisbo de que vaya a converger en un plazo razonable.

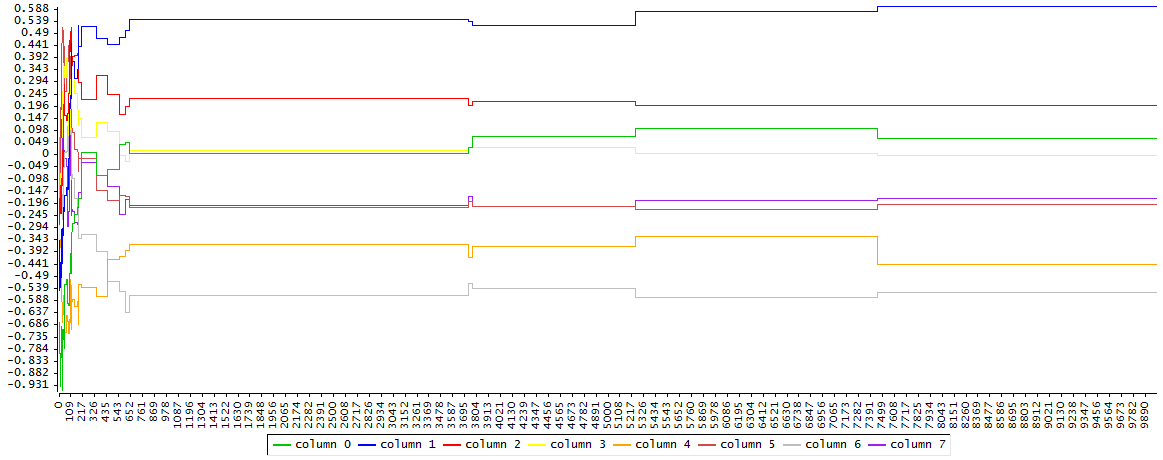
Esto indica que hay que reducir el tamaño de paso, por ejemplo a 0.1

mejora en cuanto a convergencia pero el ratio de aceptación sigue siendo insignificante.

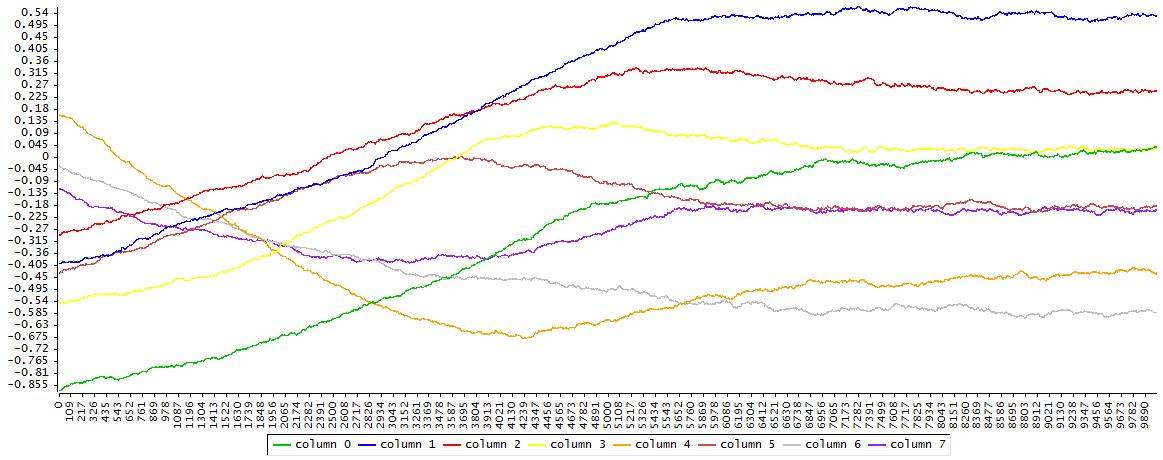
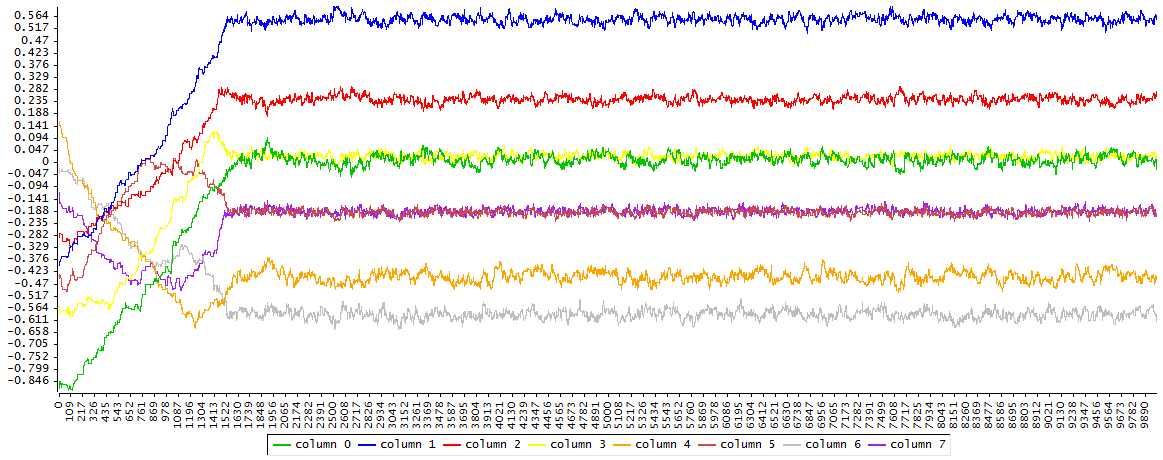
Hay que seguir reduciendo el tamaño de paso y se intenta con 0.001

El proceso tiene ahora un aspecto de paseo aleatorio no estacionario y la convergencia se hace ahora muy lenta, lo que indica que el tamaño de paso es demasiado pequeño.

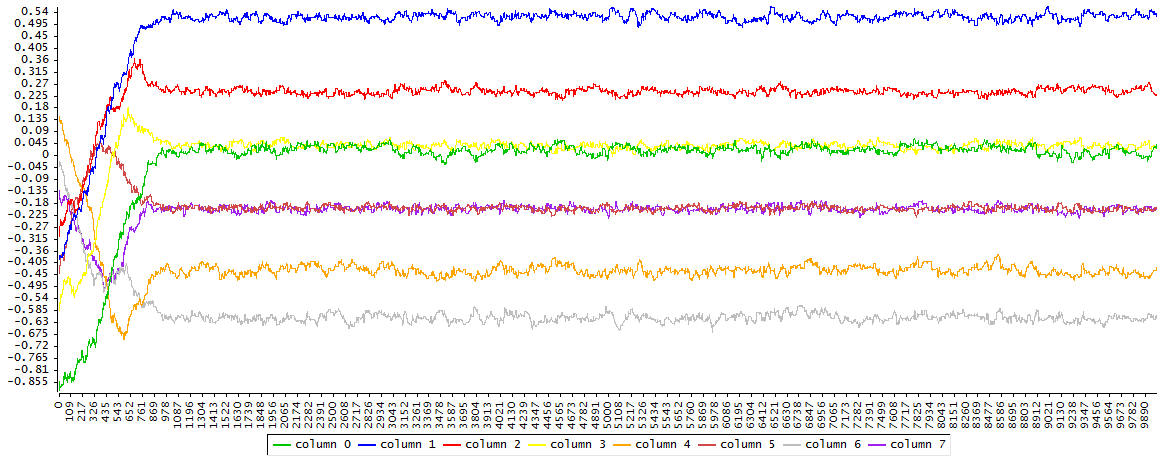
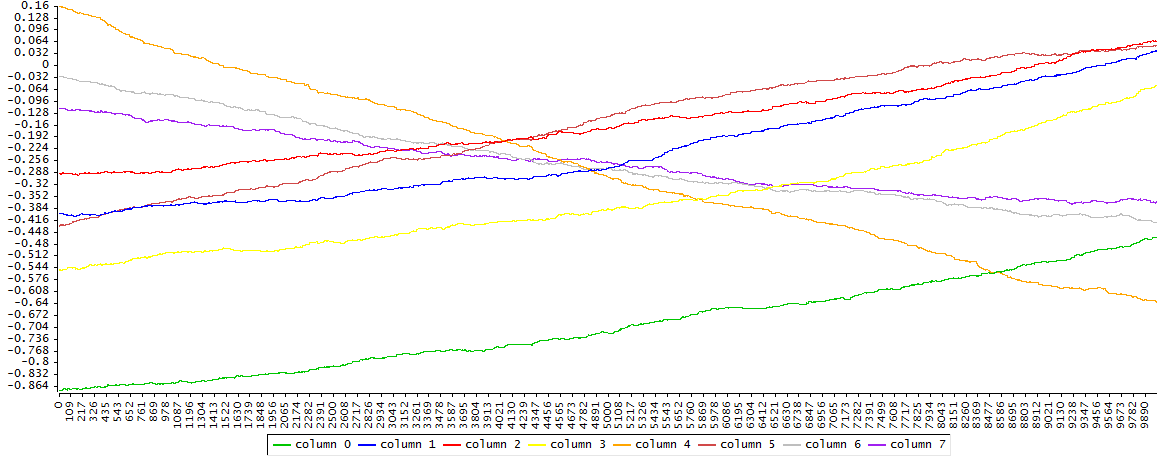
Después de varias pruebas se observa que con tamaño de paso 0.08 se obtiene un ratio de aceptación cercao al objetivo de 1/4

Ya no hay dudas respecto a la convergencia pues la verosimilitud en la media es mayor que con los parámetros ARMA reales. Para hacer inferencia robusta hay que tener en cuenta que se necesita pasar un thinning de 4, es decir, tomar 1 de cada 4 simulaciones, por lo que hay que generar 4 veces más de las necesarias.

Simulación con Random Walk Multiple Try Metropolis

El método RWMTM aumenta el ratio de aceptación pero es igual de sensible al tamaño de paso que el RWMH, si no lo es más.

Tamaño de paso 0.1

Tamaño de paso 0.01

Tamaño de paso 0.001