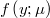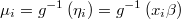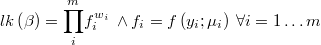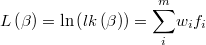close Warning: Can't synchronize with repository "(default)" (/var/svn/tolp does not appear to be a Subversion repository.). Look in the Trac log for more information.

Version 20 (modified by Víctor de Buen Remiro, 14 years ago) (diff)

--

  1. Package GrzLinModel
    1. Weighted Generalized Regresions
      1. Weighted Normal Regresion
      2. Weighted Poisson Regresion
      3. Weighted Qualitative Regresion

Package GrzLinModel

Max-likelihood and bayesian estimation of ​generalized linear models with scalar prior information and constraining linear inequations.

Weighted Generalized Regresions

Abstract class GrzLinModel::@WgtReg is the base to inherit weighted generalized linear regressions as poisson, binomial, normal or any other, given just the scalar link function 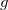g and the density function f .

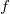In a weighted regression each row of input data has a distinct weight in the likelihood function. For example, it can be very usefull to handle with data extrated from an stratified sample.

Let be

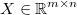  • X\in\mathbb{R}^{m\times n} the regression input matrix
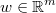  • w\in\mathbb{R}^{m} the vector of weights of each register
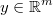  • y\in\mathbb{R}^{m} the regression output matrix
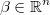  • \beta\in\mathbb{R}^{n} the regression coefficients
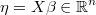  • \eta=X\beta\in\mathbb{R}^{n} the linear prediction
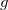  • g the link function
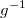  • g^{-1} the inverse-link or mean function
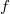  • f the density function of a distribution of the ​exponential family

Then we purpose that the average of the output is the inverse of the link function applyied to the linear predictor

E\left[y\right]=\mu=g^{-1}\left(X\beta\right)

The density function becomes as a real valuated function of at least two parameters

f\left(y;\mu\right)

For each row 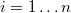i=1 \dots n we will know the output 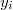y_i and the average

\mu_i=g^{-1}\left(\eta_i\right)=g^{-1}\left(x_i\beta\right)

Each particular distribution may have its own additional parameters which will be treated as a different Gibbs block and should implement next methods in order to be able of build both bayesian and max-likelihood estimations

  • the mean function:

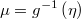
    \mu = g^{-1}\left(\eta\right)

  • the log-density function:

    \ln f

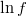
  • the first and second partial derivatives of log-density function respect to the linear prediction

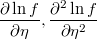
    \frac{\partial\ln f}{\partial\eta},\frac{\partial^{2}\ln f}{\partial\eta^{2}}

The likelihood function of the weigthed regression is then

lk\left(\beta\right)=\overset{m}{\underset{i}{\prod}}f_{i}^{w_{i}}\:\wedge f_{i}=f\left(y_{i};\mu_{i}\right)\:\forall i=1\ldots m

and its logarithm

L\left(\beta\right)=\ln\left(lk\left(\beta\right)\right)=\overset{m}{\underset{i}{\sum}}w_{i}f_{i}

The gradient of the logarithm of the likelihood function will be

\frac{\partial L\left(\beta\right)}{\partial\beta_{j}}=\frac{\partial L\left(\beta\right)}{\partial\eta_{i}}\frac{\partial\eta_{i}}{\partial\beta_{j}}=\overset{m}{\underset{i}{\sum}}w_{i}\frac{\partial\ln f_{i}}{\partial\eta_{i}}x_{ij}

and the hessian is

\frac{\partial L\left(\beta\right)}{\partial\beta_{i}\partial\beta_{j}}=\underset{k}{\sum}w_{k}\frac{\partial^{2}\ln f_{k}}{\partial\eta_{k}^{2}}x_{ik}x_{jk}

This class also implements these common features

  • scalar prior information of type normal or uniform, truncated or not in both cases, and
  • linear constraining inequations over linear parameters

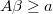
    A \beta \ge a

Weighted Normal Regresion

Is implemented in GrzLinModel::@WgtNormal There is an example of use in test_0001/test.tol

In this case we have

  • the identity as link function and mean function

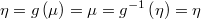
    \eta = g\left(\mu\right)= \mu = g^{-1}\left(\eta\right) = \eta

  • the density function has the variance as extra parameter

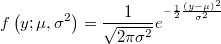
    f\left(y;\mu,\sigma^{2}\right)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{^{-\frac{1}{2}\frac{\left(y-\mu\right)^{2}}{\sigma^{2}}}}

  • the density function will be then

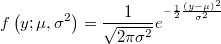
    f\left(y;\mu,\sigma^{2}\right)=\frac{1}{\sqrt{2\pi\sigma^{2}}}e^{^{-\frac{1}{2}\frac{\left(y-\mu\right)^{2}}{\sigma^{2}}}}

  • the log-density function will be then

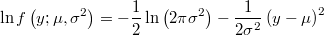
    \ln f\left(y;\mu,\sigma^{2}\right)= -\frac{1}{2}\ln\left(2\pi\sigma^{2}\right)-\frac{1}{2\sigma^{2}}\left(y}-\mu\right)^{2}

  • the partial derivatives of log-density function respect to the linear prediction is

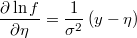
    \frac{\partial\ln f}{\partial\eta}=\frac{1}{\sigma^{2}}\left(y-\eta\right)

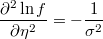
    \frac{\partial^{2}\ln f}{\partial\eta^{2}}=-\frac{1}{\sigma^{2}}

Weighted Poisson Regresion

It will be implemented in GrzLinModel::@WgtPoisson but is not available yet. There is an example of use in test_0002/test.tol

In this case we have

  • the link function

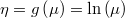
    \eta = g\left(\mu\right)=\ln\left(\mu\right)

  • the mean function

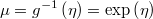
    \mu = g^{-1}\left(\eta\right)=\exp\left(\eta\right)

  • the probability mass function

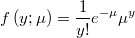
    f\left(y;\mu\right)=\frac{1}{y!}e^{-\mu}\mu^{y}

  • and its logarithm will be

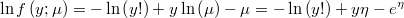
    \ln f\left(y;\mu\right)=-\ln\left(y!\right)+y\ln\left(\mu\right)-\mu = -\ln\left(y!\right)+y\eta-e^{\eta}

  • the partial derivatives of log-density function respect to the linear prediction is

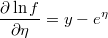
    \frac{\partial\ln f}{\partial\eta}=y-e^{\eta}

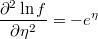
    \frac{\partial^{2}\ln f}{\partial\eta^{2}}=-e^{\eta}

Weighted Qualitative Regresion

For boolean and qualitative response outputs like logit or probit there is an specialization on package QltvRespModel